Câu hỏi:
2 năm trước
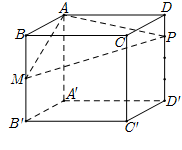
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có diện tích đáy bằng \(12\) và chiều cao bằng \(6\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(CB,\,\,CA\) và \(P,\,\,Q,\,\,R\) lần lượt là tâm các hình bình hành \(ABB'A'\), \(BCC'B'\), \(CAA'C'\). Thể tích của khối đa diện \(PQRABMN\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
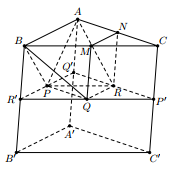
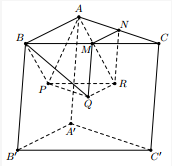
Gọi \(P',\,\,Q',\,\,R'\) lần lượt là giao điểm của mặt phẳng \(\left( {PQR} \right)\) với các cạnh \(CC',\,\,AA',\,\,BB'\).
Dễ dàng chứng minh được \(P',\,\,Q',\,\,R'\) tương ứng là trung điểm của các cạnh \(CC',\,\,AA',\,\,BB'\), đồng thời \(P,\,\,Q,\,\,R\) lần lượt là trung điểm của các cạnh \(Q'R',\,\,R'P',\,\,P'Q'\).
Đặt \(V = {V_{ABC.Q'R'P'}}\).
Ta có: \({S_{R'PQ}} = \dfrac{1}{4}{S_{R'Q'P'}}\) nên \({V_{B.R'PQ}} = \dfrac{1}{4}{V_{B.R'Q'P'}} \)\(= \dfrac{1}{4}.\dfrac{1}{3}V = \dfrac{1}{{12}}V\)
Tương tự ta có: \({V_{A.Q'PR}} = \dfrac{1}{{12}}V\).
Ta có: \({S_{MNC}} = {S_{QRP'}} = \dfrac{1}{4}{S_{ABC}}\) nên \({V_{CMN.P'QR}} = \dfrac{V}{4}\)
Vậy \(V{V_{PQRABMN}} = V - {V_{B.R'PQ}} - {V_{A.Q'PR}} - {V_{CMN.P'QR}} = V - 2.\dfrac{V}{{12}} - \dfrac{V}{4} = \dfrac{{7V}}{{12}} = \dfrac{7}{2}.\dfrac{1}{2}.12.6 = 21\).
Hướng dẫn giải:
- Gọi \(P',\,\,Q',\,\,R'\) lần lượt là giao điểm của mặt phẳng \(\left( {PQR} \right)\) với các cạnh \(CC',\,\,AA',\,\,BB'\). Chứng minh \(P',\,\,Q',\,\,R'\) tương ứng là trung điểm của các cạnh \(CC',\,\,AA',\,\,BB'\), đồng thời \(P,\,\,Q,\,\,R\) lần lượt là trung điểm của các cạnh \(Q'R',\,\,R'P',\,\,P'Q'\).
- Đặt \(V = {V_{ABC.Q'R'P'}}\), tính \({V_{B.R'PQ}}\), \({V_{A.Q'PR}}\), \({V_{CMN.P'QR}}\) theo \(V\).
- Tính \({V_{PQRABMN}} = V - {V_{B.R'PQ}} - {V_{A.Q'PR}} - {V_{CMN.P'QR}}\) theo \(V\).
- Tính \(V\) và suy ra \({V_{PQRABMN}}\).
