Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy $ABC$ là tam giác vuông tại $B$, \(\widehat {ACB} = {60^0}\), cạnh \(BC = a\), đường chéo \(A'B\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \({30^0}\). Thể tích khối lăng trụ \(ABC.A'B'C'\) là:
Trả lời bởi giáo viên
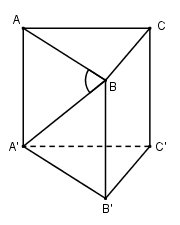
Vì \(AA' \bot \left( {ABC} \right) \Rightarrow AB\) là hình chiếu vuông góc của $A'B$ lên \( (ABC)\Rightarrow \widehat {\left( {A'B;\left( {ABC} \right)} \right)} = \widehat {\left( {A'B;AB} \right)} = \widehat {A'BA} = {30^0}\)
Xét tam giác vuông $ABC$ có: \(AB = BC.\tan 60 = a\sqrt 3 \)
\(AA' \bot \left( {ABC} \right) \supset AB \Rightarrow AA' \bot AB \Rightarrow \Delta ABA'\) vuông tại $A$ \( \Rightarrow AA' = AB.\tan \widehat {A'BA} = a\sqrt 3 .\tan 30 = a\sqrt 3 .\dfrac{1}{{\sqrt 3 }} = a\)
\({S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}a\sqrt 3 .a = \dfrac{{{a^2}\sqrt 3 }}{2}\)
Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{2}\)
Hướng dẫn giải:
- Xác định góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\): góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính độ dài đường cao \(AA'\) và diện tích đáy \({S_{\Delta ABC}}\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\).