Hàm số y=logax và y=logbx có đồ thị như hình vẽ bên:
Đường thẳng y=3 cắt hai đồ thị tại các điểm có hoành độ x1,x2. Biết rằng x2=2x1, giá trị của ab bằng:
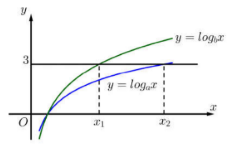
Dựa vào đồ thị hàm số ta thấy x1 là nghiệm của phương trình hoành độ giao điểm logbx1=3⇔x1=b3.
Và x2 là nghiệm của phương trình hoành độ giao điểm logax2=3⇔x2=a3.
Theo đề bài ta có: x2=2x1⇒a3=2b3⇔a3b3=2⇔ab=3√2.
Hàm số y=loge3(x−1) nghịch biến trên khoảng nào dưới đây?
Xét hàm số y=loge3(x−1) có TXĐ: D=(1;+∞) và a=e3<1
⇒ Hàm số nghịch biến trên (1;+∞).
Tìm tất cả các giá trị của tham số m để hàm số y=log2020(mx−m+2) xác định trên [1;+∞).
ĐKXĐ: mx−m+2>0⇔m(x−1)>−2
Để hàm số xác định trên [1;+∞) thì m(x−1)>−2(∗),∀x≥1
+) x=1⇒ (*) ⇔0m>−2 đúng với mọi m
+) x>1⇒ (*) ⇔m>−2x−1, ∀x>1 (2*).
Xét hàm số f(x)=−2x−1∀x>1ta có f′(x)=2(x−1)2>0∀x∈(1;+∞).
BBT:
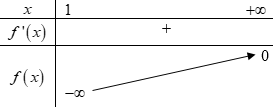
Dựa vào BBT ⇒m≥0.
Vậy để hàm số y=log2020(mx−m+2) xác định trên [1;+∞) thì m≥0.
Đồ thị của hàm số y=f(x) đối xứng với đồ thị của hàm số y=ax(a>0,a≠1) qua điểm M(1;1). Giá trị của hàm số y=f(x) tại x=2+loga12020 bằng:
Lấy điểm A(x0;ax0)∈(C1) (đồ thị của hàm số y=ax. Gọi B là điểm đối xứng của A qua M(1;1).
⇒{xB=2xM−xA=2−x0yB=2yM−yA=2−ax0⇒x0=2−xB⇒yB=2−a2−xB
⇒ Hàm số y=f(x)=2−a2−x
⇒f(2+loga12020)=2−a2−(2+loga12020)=2−aloga20220=2−2020=−2018.
Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị y=logax,y=logbx và trục hoành lần lượt tại A,B và H phân biệt ta đều có 3HA=4HB (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
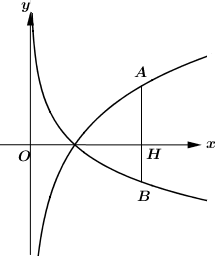
Gọi H(x0;0)(x0>1) ta có: A(x0;logax0);B(x0;logbx0).
⇒HA=logax0; HB=−logbx0 (do logax0>0,logbx0<0).
Theo bài ra ta có: 3HA=4HB⇔3logax0=−4logbx0.
⇔3logax0+4logbx0=0⇔3logx0a+4logx0b=0⇔3logx0b+4logx0alogx0b.logx0a=0⇔logx0b3+logx0a4=0⇔logx0a4b3=0⇔a4b3=1
Cho hàm số f(x)=ln(ex+m) có f′(−ln2)=32. Mệnh đề nào dưới đây đúng?
Ta có: f(x)=ln(ex+m)
Điều kiện: ex+m>0.
⇒f′(x)=exex+m⇒f′(−ln2)=32⇔e−ln2e−ln2+m=32⇔2.e−ln2=3.e−ln2+3m⇔2.2−lne=3.2−lne+3m⇔2.12−3.12=3m⇔m=−16.⇒m∈(−2;0).
Xét các số thực a, b thỏa mãn a>b>1. Tìm giá trị nhỏ nhất Pmin của biểu thức P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\left( {\dfrac{a}{b}} \right).
Ta có P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\dfrac{a}{b}
\Leftrightarrow P = 4\log _{\frac{a}{b}}^2a + 3\left( {{{\log }_b}a - 1} \right) \Leftrightarrow P = \dfrac{4}{{{{\left( {1 - {{\log }_a}b} \right)}^2}}} + 3\left( {\dfrac{1}{{{{\log }_a}b}} - 1} \right)
Đặt {\log _a}b = t \Rightarrow 0 < t < 1 . Khi đó P = \dfrac{4}{{{{\left( {t - 1} \right)}^2}}} + \dfrac{3}{t} - 3
P' = \dfrac{{ - 8}}{{{{\left( {t - 1} \right)}^3}}} - \dfrac{3}{{{t^2}}} = 0 \Leftrightarrow 3{t^3} - {t^2} + 9t - 3 = 0 \Rightarrow t = \dfrac{1}{3}
\Rightarrow {P_{\min }} = 15.
Cho hai hàm số y = \ln \left| {\dfrac{{x - 2}}{x}} \right| và y = \dfrac{3}{{x - 2}} - \dfrac{1}{x} + 4m - 2020. Tổng tất cả các giá trị nguyên của tham số m để hai đồ thị hàm số cắt nhau tại một điểm duy nhất bằng:
ĐKXĐ: x \ne 0,\,\,x \ne 2.
Xét phương trình hoành độ giao điểm:
\begin{array}{l}\ln \left| {\dfrac{{x - 2}}{x}} \right| = \dfrac{3}{{x - 2}} - \dfrac{1}{x} + 4m - 2020\\ \Leftrightarrow \ln \left| {\dfrac{{x - 2}}{x}} \right| - \dfrac{3}{{x - 2}} + \dfrac{1}{x} = 4m - 2020\end{array}
Đặt f\left( x \right) = \ln \left| {\dfrac{{x - 2}}{x}} \right| - \dfrac{3}{{x - 2}} + \dfrac{1}{x} ta có:
\begin{array}{l}f'\left( x \right) = \dfrac{2}{{{x^2}}}:\dfrac{{x - 2}}{x} + \dfrac{3}{{{{\left( {x - 2} \right)}^2}}} - \dfrac{1}{{{x^2}}}\\f'\left( x \right) = \dfrac{2}{{x\left( {x - 2} \right)}} + \dfrac{3}{{{{\left( {x - 2} \right)}^2}}} - \dfrac{1}{{{x^2}}}\\f'\left( x \right) = \dfrac{{2x\left( {x - 2} \right) + 3{x^2} - {{\left( {x - 2} \right)}^2}}}{{{x^2}{{\left( {x - 2} \right)}^2}}}\\f'\left( x \right) = \dfrac{{2{x^2} - 4x + 3{x^2} - {x^2} + 4x - 4}}{{{x^2}{{\left( {x - 2} \right)}^2}}}\\f'\left( x \right) = \dfrac{{4{x^2} - 4}}{{{x^2}{{\left( {x - 2} \right)}^2}}} = 0 \Leftrightarrow x = \pm 1\end{array}
BBT:
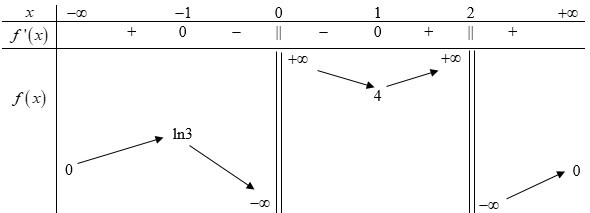
Dựa vào BBT ta thấy để phương trình có nghiệm duy nhất thì \left[ \begin{array}{l}4m - 2020 = 0\\4m - 2020 = \ln 3\\4m - 2020 = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 505\\m = \dfrac{{2020 + \ln 3}}{4} \notin \mathbb{Z}\,\,\left( {ktm} \right)\\m = 506\end{array} \right..
Vậy tổng các giá trị của m thỏa mãn yêu cầu bài toán là: 505 + 506 = 1011.
Cho x, y là các số thực thỏa mãn {\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1. Tìm giá trị nhỏ nhất {P_{\min }} của biểu thức P = 2x - y.
Điều kiện : x + y >0, x – y > 0
{\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1 \Leftrightarrow {\log _4}\left( {{x^2} - {y^2}} \right) \ge 1 \Leftrightarrow {x^2} - {y^2} \ge 4
Ta có: P = 2x - y = \dfrac{{x + y + 3(x - y)}}{2} \ge \sqrt {(x + y).3(x - y)} = \sqrt {3({x^2} - {y^2})} = \sqrt {3.4} = 2\sqrt 3
Dấu “=” xảy ra khi:
\left\{ \begin{array}{l}x + y = 3\left( {x - y} \right)\\{x^2} - {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\left( {x - y} \right)\\3{\left( {x - y} \right)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = \dfrac{2}{{\sqrt 3 }}\\x + y = 2\sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{{\sqrt 3 }} + \sqrt 3 \\y = \sqrt 3 - \dfrac{1}{{\sqrt 3 }}\end{array} \right.
Vậy Min\,P = 2\sqrt 3 .

