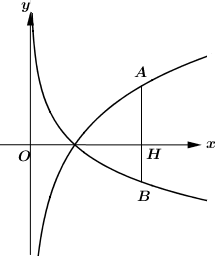
Cho \(a\) và \(b\) là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị \(y = {\log _a}x,\,\,y = {\log _b}x\) và trục hoành lần lượt tại \(A,\,\,B\) và \(H\) phân biệt ta đều có \(3HA = 4HB\) (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Gọi \(H\left( {{x_0};0} \right)\,\,\left( {{x_0} > 1} \right)\) ta có: \(A\left( {{x_0};{{\log }_a}{x_0}} \right);\,\,B\left( {{x_0};{{\log }_b}{x_0}} \right)\).
\( \Rightarrow HA = {\log _a}{x_0}\); \(HB = - {\log _b}{x_0}\) (do \({\log _a}{x_0} > 0,\,\,{\log _b}{x_0} < 0\)).
Theo bài ra ta có: \(3HA = 4HB\)\( \Leftrightarrow 3{\log _a}{x_0} = - 4{\log _b}{x_0}\).
\(\begin{array}{l} \Leftrightarrow 3{\log _a}{x_0} + 4{\log _b}{x_0} = 0\\ \Leftrightarrow \dfrac{3}{{{{\log }_{{x_0}}}a}} + \dfrac{4}{{{{\log }_{{x_0}}}b}} = 0\\ \Leftrightarrow \dfrac{{3{{\log }_{{x_0}}}b + 4{{\log }_{{x_0}}}a}}{{{{\log }_{{x_0}}}b.{{\log }_{{x_0}}}a}} = 0\\ \Leftrightarrow {\log _{{x_0}}}{b^3} + {\log _{{x_0}}}{a^4} = 0\\ \Leftrightarrow {\log _{{x_0}}}{a^4}{b^3} = 0\\ \Leftrightarrow {a^4}{b^3} = 1\end{array}\)
Hướng dẫn giải:
- Gọi \(H\left( {{x_0};0} \right)\,\,\left( {{x_0} > 1} \right)\), xác định tọa độ các điểm \(A,\,\,B\).
- Tính \(HA,\,\,HB\) sau đó biến đổi tìm mối liên hệ giữa \(a\) và \(b\).

