Trả lời bởi giáo viên
Đáp án đúng: b
Bước 1:
Ta có: sinx=12⇔sinx=sinπ6
Bước 2:
⇔[x=π6+k2πx=5π6+k2π(k∈Z)
Bước 3:
+) Xét x=π6+k2π
Ta có −π2≤x≤π2⇔−π2≤π6+k2π≤π2
−2π3≤k2π≤π3⇔−2π3.2π≤k≤π3.2π⇔−13≤k≤16
Mà k∈Z⇒k=0. Thay vào x ta được: x=π6
+) Xét x=5π6+k2π
−π2≤x≤π2⇔−π2≤5π6+k2π≤π2⇔−4π3≤k2π≤−π3⇔−4π3.2π≤k≤−π3.2π⇔−23≤k≤−16
Mà k∈Z nên không có giá trị k thỏa mãn
Vậy phương trình ban đầu có nghiệm duy nhất là x=π6
Hướng dẫn giải:
Bước 1: Đưa 12 về dạng sinα
Sử dụng máy tính để tìm α:
SHIFT => MODE => 4 : chuyển về chế độ Radian
SHIFT => SIN => (1/2) =>"="
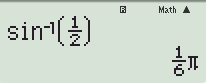
Bước 2: Giải phương trình lượng giác cơ bản sinx=sinα⇔[x=α+k2πx=π−α+k2π
Bước 3: Xét từng họ nghiệm và thay vào −π2≤x≤π2 để tìm k sau đó thay k ngược lại để tìm x.

