Bài toán cực trị có tham số đối với một số hàm số cơ bản
Kỳ thi ĐGTD ĐH Bách Khoa
Cho hàm số $y = f\left( x \right)$ liên tục trên $R$ và có đồ thị như hình vẽ bên, một hàm số $g\left( x \right)$ xác định theo $f\left( x \right)$ có đạo hàm $g'\left( x \right) = f\left( x \right) + m$. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $g\left( x \right)$ có duy nhất một cực trị.
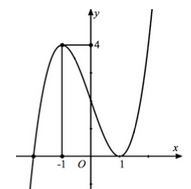
Hàm số $g\left( x \right)$ có duy nhất một cực trị $ \Leftrightarrow $ pt $g'\left( x \right) = 0$ có đúng một nghiệm \(x_0\) thỏa mãn \(g'(x)\) đổi dấu qua nghiệm đó.
Theo đề bài ta có: $g'\left( x \right) = f\left( x \right) + m$ $ \Rightarrow g'\left( x \right) = 0 \Leftrightarrow f\left( x\right) + m = 0 \Leftrightarrow f\left( x \right) = - m$ $ \Rightarrow $ Số nghiệm của pt $g'\left( x \right) = 0$ là số giao điểm của đồ thị hàm số $y = f\left( x \right)$ và đường thẳng $y = - m$.
Quan sát đồ thị ta thấy đường thẳng $y = - m$ cắt đồ thị hàm số $y = f\left( x \right)$ tại một điểm duy nhất
$ \Leftrightarrow \left[ \begin{gathered} - m < 0 \hfill \\ - m > 4 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}m > 0 \hfill \\ m < - 4 \hfill \\ \end{gathered} \right.$.
Ngoài ra, với \(m=0\) hoặc \(m=-4\) thì đồ thị hàm số \(y=f(x)\) có hai điểm chung với đường thẳng \(y=m\) nhưng một điểm là điểm tiếp xúc nên phương trình \(g'(x)=0\) có hai nghiệm phân biệt, trong đó có một nghiệm kép và một nghiệm đơn.
Nên trong trường hợp này, hàm số \(y=g(x)\) vẫn chỉ có một cực trị.
Vậy \(m \ge 0 \) hoặc \( m \le - 4 \).
Cho hàm số $y = {x^3} + 6{x^2} + 3\left( {m + 2} \right)x - m - 6$ với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số có hai điểm cực trị ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$.
Ta có $y' = 3{x^2} + 12x + 3\left( {m + 2} \right) = 3\left[ {{x^2} + 4x + \left( {m + 2} \right)} \right].$
Yêu cầu bài toán $ \Leftrightarrow y' = 0$ có hai nghiệm phân biệt ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$
- Hàm số có hai điểm cực trị \( \Leftrightarrow \Delta ' = 4 - \left( {m + 2} \right) = 2 - m > 0 \Leftrightarrow m < 2\)
Hai điểm cực trị thỏa mãn \({x_1} < - 1 < {x_2}\) \( \Leftrightarrow \) phương trình \(y' = 0\) có hai nghiệm phân biệt\( \Leftrightarrow y'\left( { - 1} \right) < 0 \Leftrightarrow m < 1.\)
Cho hàm số $y = 2{x^3} + m{x^2} - 12x - 13$ với \(m\) là tham số thực. Tìm giá trị của $m$ để đồ thị hàm số có hai điểm cực trị thỏa mãn khoảng cách từ chúng đến trục tung bằng nhau.
Ta có $y' = 6{x^2} + 2mx - 12.$
Do $\Delta ' = {m^2} + 72 > 0,{\rm{ }}\forall m \in \mathbb{R}$ nên hàm số luôn có hai điểm cực trị \({x_1},{\rm{ }}{x_2}\) với \({x_1},{\rm{ }}{x_2}\) là hai nghiệm của phương trình \(y' = 0\).
Theo định lí Viet, ta có ${x_1} + {x_2} = - \dfrac{m}{3}.$
Gọi $A\left( {{x_1};{y_1}} \right)$ và $B\left( {{x_2};{y_2}} \right)$ là hai điểm cực trị của đồ thị hàm số.
Yêu cầu bài toán \( \Leftrightarrow \left| {{x_1}} \right| = \left| {{x_2}} \right| \Leftrightarrow {x_1} = - {x_2}\) (do \({x_1} \ne {x_2}\))
$ \Leftrightarrow {x_1} + {x_2} = 0 \Leftrightarrow - \dfrac{m}{3} = 0 \Leftrightarrow m = 0.$
Cho hàm số \(y = {x^3} - 3m{x^2} + 4{m^2} - 2\) với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số có hai điểm cực trị \(A,{\rm{ }}B\) sao cho \(I\left( {1;0} \right)\) là trung điểm của đoạn thẳng \(AB\).
Ta có \(y' = 3{x^2} - 6mx = 3x\left( {x - 2m} \right);{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2m\end{array} \right..\)
Đề đồ thị hàm số có hai điểm cực trị \( \Leftrightarrow m \ne 0\).
Khi đó tọa độ hai điểm cực trị là \(A\left( {0;4{m^2} - 2} \right)\) và \(B\left( {2m;4{m^2} - 4{m^3} - 2} \right)\).
Do \(I\left( {1;0} \right)\) là trung điểm của \(AB\) nên \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_I}\\{y_A} + {y_B} = 2{y_I}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}0 + 2m = 2\\\left( {4{m^2} - 2} \right) + \left( {4{m^2} - 4{m^3} - 2} \right) = 0\end{array} \right. \Leftrightarrow m = 1:\) thỏa mãn.
Gọi \({m_0}\) là giá trị của \(m\) thỏa mãn đồ thị hàm số \(y = \dfrac{{{x^2} + mx - 5}}{{{x^2} + 1}}\) có hai điểm cực trị \(A,B\) sao cho đường thẳng \(AB\) đi qua điểm\(I\left( {1; - 3} \right)\). Khẳng định nào sau đây là đúng?
TXĐ: \(D = \mathbb{R}\)
Ta có \(y = \dfrac{{{x^2} + mx - 5}}{{{x^2} + 1}} = 1 + \dfrac{{mx - 6}}{{{x^2} + 1}}\)
Suy ra \(y' = \dfrac{{m\left( {{x^2} + 1} \right) - 2x\left( {mx - 6} \right)}}{{{{\left( {{x^2} + 1} \right)}^2}}} = \dfrac{{ - m{x^2} + 12x + m}}{{{{\left( {{x^2} + 1} \right)}^2}}}\)
Để hàm số đã cho có hai cực trị thì phương trình \(y' = 0\) có hai nghiệm phân biệt hay \( - m{x^2} + 12x + m = 0\) có hai nghiệm phân biệt. Ta có \(\Delta ' = 36 + {m^2} > 0;\,\forall m\) nên hàm số luôn có hai cực trị.
Phương trình đường thẳng \(AB\) qua hai điểm cực trị là \(y = \dfrac{{2\left( { - m} \right)x - 4.\left( { - 5} \right)}}{{ - 4}} = \dfrac{m}{2}x - 5\)
Đường thẳng \(AB\) qua điểm \(I\left( {1; - 3} \right)\) nên \( - 3 = \dfrac{m}{2}.1 - 5 \Leftrightarrow m = 4\)
Suy ra \({m_0} = 4\)
Hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) (với \(m\) là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?
Hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) có TXĐ \(D = \mathbb{R}\).
Xét hàm số \(g\left( x \right) = \dfrac{x}{{{x^2} + 1}} - m\) ta có:
\(g'\left( x \right) = \dfrac{{{x^2} + 1 - x.2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} = \dfrac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0 \Leftrightarrow x = \pm 1\).
\( \Rightarrow \) Hàm số \(y = g\left( x \right)\) có 2 điểm cực trị.
Xét phương trình hoành độ giao điểm \(\dfrac{x}{{{x^2} + 1}} - m = 0 \Leftrightarrow \dfrac{{x - m\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = 0 \Leftrightarrow - m{x^2} + x - m = 0\), phương trình có \(\Delta = 1 - 4{m^2}\) chưa xác định dấu nên có tối đa 2 nghiệm.
Vậy hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) có tối đa \(2 + 2 = 4\) cực trị.
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \dfrac{{{x^2} + mx + 2m}}{{x + 1}}\) có hai điểm cực trị \(A,\,\,B\) và tam giác \(OAB\) vuông tại O. Tổng tất cả các phần tử của \(S\) là:
ĐKXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(y = \dfrac{{{x^2} + mx + 2m}}{{x + 1}} = x + m - 1 + \dfrac{{m + 1}}{{x + 1}}\).
\( \Rightarrow y' = 1 - \dfrac{{m + 1}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{{x^2} + 2x - m}}{{{{\left( {x + 1} \right)}^2}}}\)
Để hàm số đã cho có 2 cực trị thì phương trình \(y' = 0\) phải có 2 nghiệm phân biệt khác \( - 1\).
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = 1 + m > 0\\1 - 2 - m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - 1\\m \ne - 1\end{array} \right. \Leftrightarrow m > - 1.\)
Khi đó, giả sử \({x_1},\,\,{x_2}\) là nghiệm phân biệt của phương trình \(y' = 0\), áp dụng định lí Vi-ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}.{x_2} = - m\end{array} \right..\)
Đặt \(A\left( {{x_1};{x_1} + m - 1 + \dfrac{{m + 1}}{{{x_1} + 1}}} \right),\,\,B\left( {{x_2};{x_2} + m - 1 + \dfrac{{m + 1}}{{{x_2} + 1}}} \right)\) là hai điểm cực trị của hàm số.
Để tam giác \(OAB\) vuông tại \(O\) thì \(\overrightarrow {OA} .\overrightarrow {OB} = 0\).
\(\begin{array}{l} \Leftrightarrow {x_1}.{x_2} + \left( {{x_1} + m - 1 + \dfrac{{m + 1}}{{{x_1} + 1}}} \right)\left( {{x_2} + m - 1 + \dfrac{{m + 1}}{{{x_2} + 1}}} \right) = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\left( {\dfrac{{{x_1}}}{{{x_2} + 1}} + \dfrac{{{x_2}}}{{{x_1} + 1}}} \right)\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}}} \right) + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\dfrac{{x_1^2 + x_2^2 + {x_1} + {x_2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}}\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\dfrac{{{x_1} + {x_2} + 2}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\dfrac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} + {x_1} + {x_2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}}\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\dfrac{{{x_1} + {x_2} + 2}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} = 0\\ \Leftrightarrow - 2m - 2\left( {m - 1} \right) + \left( {m + 1} \right).\dfrac{{2 + 2m}}{{ - m - 1}} + {\left( {m - 1} \right)^2} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{ - m - 1}} = 0\\ \Leftrightarrow - 2m - 2m + 2 - 2 - 2m + {m^2} - 2m + 1 - m - 1 = 0\\ \Leftrightarrow {m^2} - 9m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 9\end{array} \right.\,\,\left( {tm} \right)\end{array}\)
\( \Rightarrow S = \left\{ {0;9} \right\}\).
Vậy tổng tất cả các phần tử của S là \(9\).
Có bao nhiêu giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1\) có hai điểm cực trị nằm về hai phía của trục hoành.
Để đồ thị hàm số \(y = m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1\) có hai điểm cực trị nằm về hai phía của trục hoành thì phương trình \(m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1 = 0\,\,\left( * \right)\) phải có 3 nghiệm phân biệt.
Ta có:
\(\begin{array}{l}\,\,\,\,\,m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1 = 0\\ \Leftrightarrow \left( {x - 1} \right)\left[ {m{x^2} - \left( {m - 1} \right)x + m + 1} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\m{x^2} - \left( {m - 1} \right)x + m + 1 = 0\,\,\,\left( {**} \right)\end{array} \right.\end{array}\)
Để (*) có ba nghiệm phân biệt thì (**) phải có 2 nghiệm phân biệt khác 1.
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m.1 - \left( {m - 1} \right).1 + m + 1 \ne 0\\\Delta = {\left( {m - 1} \right)^2} - 4m\left( {m + 1} \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m - m + 1 + m + 1 \ne 0\\{m^2} - 2m + 1 - 4{m^2} - 4m > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\ - 3{m^2} - 6m + 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\\dfrac{{ - 3 - 2\sqrt 3 }}{3} < m < \dfrac{{ - 3 + 2\sqrt 3 }}{3}\end{array} \right.\end{array}\)
Mà \(m \in \mathbb{Z}\) \( \Rightarrow m = - 1\).
Vậy có 1 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
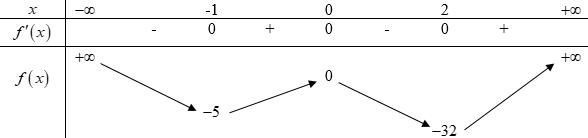
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị?
Xét hàm số \(f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\) ta có
\(\begin{array}{l}f'\left( x \right) = 12{x^3} - 12{x^2} - 24x\\f'\left( x \right) = 0 \Leftrightarrow 12{x^3} - 12{x^2} - 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\end{array} \right.\end{array}\)
BBT:
Ta có đồ thị \(y = f\left( x \right)\,\,\left( C \right)\) như sau:
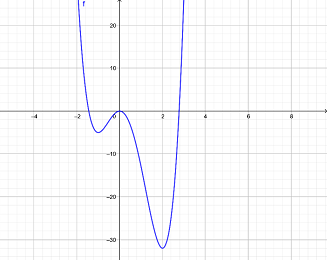
Để \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị thì:
TH1: \(\left( C \right)\) cắt đường thẳng \(y = - m\) tại 2 điểm phân biệt khác cực trị
\( \Leftrightarrow \left[ \begin{array}{l} - m > 0\\ - 32 < - m < - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\5 < m < 32\end{array} \right.\)
Mà \(m \in {\mathbb{Z}^ + }\, \Rightarrow m \in \left\{ {6;7;...;31} \right\}\) : 26 giá trị.
TH2: \(\left( C \right)\) cắt đường thẳng \(y = - m\) tại 3 điểm phân biệt, trong đó có 1 cực trị
\( \Leftrightarrow \left[ \begin{array}{l} - m = 0\\ - m = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\,(L)\\m = 5\,(TM)\end{array} \right.\)
Vậy, có tất cả 27 giá trị của m thỏa mãn.
Cho hàm số \(f\left( x \right) = \dfrac{1}{3}{x^3} + m{x^2} + \left( {{m^2} - 4} \right)x + 1\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {\left| x \right|} \right)\) có đúng 3 điểm cực trị?
Bước 1:
Số điểm cực trị của hàm số \(y = f\left( {\left| x \right|} \right)\) là \(2m + 1\) trong đó \(m\) là số điềm cực trị dương của hàm số \(y = f\left( x \right)\).
Do đó để hàm số \(y = f\left( {\left| x \right|} \right)\) có đúng 3 điểm cực trị thì \(m = 1 \Rightarrow \) hàm số \(y = f\left( x \right)\) phải có 1 điểm cực trị dương (*).
Bước 2:
Ta có: \(f'\left( x \right) = {x^2} + 2mx + {m^2} - 4\).
Xét \(f'\left( x \right) = 0\) có \(\Delta ' = {m^2} - {m^2} + 4 > 0\,\,\forall m\) nên \(f'\left( x \right) = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = - m + 2\\{x_2} = - m - 2\end{array} \right.\).
Bước 3:
\(\left( * \right) \Rightarrow - m - 2 \le 0 < - m + 2 \Leftrightarrow - 2 \le m < 2\).
Mà \(m \in \mathbb{Z}\) \( \Rightarrow m \in \left\{ { - 2; - 1;0;1} \right\}\).
Vậy có 4 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Gọi k là số giá trị nguyên của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - {x^2} \)\(+ \left( {{m^2} - 8m + 16} \right)x - 31\) có cực trị. Tìm k.
Đáp án:
Đáp án:
Ta có: \(y' = {x^2} - 2x + {m^2} - 8m + 16\).
Để hàm số đã cho có cực trị thì phương trình \(y' = 0\) phải có 2 nghiệm phân biệt.
\(\begin{array}{l} \Rightarrow \Delta ' = 1 - {m^2} + 8m - 16 > 0\\ \Leftrightarrow - {m^2} + 8m - 15 > 0\\ \Leftrightarrow 3 < m < 5\end{array}\)
Mà \(m \in \mathbb{Z} \Rightarrow m = 4\).
Vậy có 1 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
$=>k=1$

