Trong không gian với hệ trục tọa độ $Oxyz$, cho mặt phẳng $(P): 2 x-y-2 z-2=0$ và mặt phẳng $(Q): 2 x-y-2 z+10=0$ song song với nhau. Biết $A(1 ; 2 ; 1)$ là điểm nằm giữa hai mặt phẳng $(P)$ và $(Q)$. Gọi $(S)$ là mặt cầu qua $A$ và tiếp xúc với cả hai mặt phẳng $(P)$ và $(Q)$. Biết rằng khi $(S)$ thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính $r$ của đường tròn đó
$r=\dfrac{4 \sqrt{2}}{3}$
$r=\dfrac{4 \sqrt{2}}{3}$
$r=\dfrac{4 \sqrt{2}}{3}$
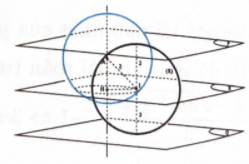
Bước 1: Tính $d((P),(Q))$
Ta thấy $M(1 ; 0 ; 0)$ là một điểm thuộc $(P)$
Vì \((P)//(Q)\) nên \(d((P),(Q)) = d(M,(Q)) \)\(= \dfrac{{|2 + 10|}}{{\sqrt {{2^2} + {{( - 1)}^2} + {{( - 2)}^2}} }} = 4\)
Bước 2: Giả sử $I(a ; b ; c)$ là tâm của $(S)$. Chứng minh $I$ luôn thuộc mặt phẳng $(R)$
Giả sử $I(a ; b ; c)$ là tâm của $(S)$. Vì $(S)$ tiếp xúc với cả $(P)$ và $(Q)$ nên bán kính mặt cầu $(S)$ là $R=\dfrac{d((P),(Q))}{2}=\dfrac{4}{2}=2$
Do đó $I A=2$ nên $I$ luôn thuộc mặt cầu $(T)$ tâm $A$, bán kính 2
Ngoài ra, $d(I,(P))=d(I,(Q)) \Leftrightarrow \dfrac{|2 a-b-2 c-2|}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}=\dfrac{|2 a-b-2 c+10|}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}$
$\Leftrightarrow|2 a-b-2 c-2|=|2 a-b-2 c+10| $
$\Leftrightarrow 2 a-b-2 c+4=0 .$
Do đó, $I$ luôn thuộc mặt phẳng $(R): 2 x-y-2 z+4$
Bước 3: Gọi $H$ là hình chiếu vuông góc của $A$ lên $(R)$.Tính HI và tính bán kính $r$
Gọi $H$ là hình chiếu vuông góc của $A$ lên $(R)$. Vì $A$,
Ta có $A H=d(A,(R))=\dfrac{|2.1-2-2.1+4|}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}=\dfrac{2}{3}$
Mà $A H \perp(R) \Rightarrow A H \perp H I$, do đó $\Delta A H I$ vuông tại $H$ nên
$H I=\sqrt{A I^{2}-A H^{2}}=\sqrt{2^{2}-\left(\dfrac{2}{3}\right)^{2}}=\dfrac{4 \sqrt{2}}{3}$
Vậy $I$ luôn thuộc đường tròn tâm $H$, nằm trên mặt phẳng $(R)$, bán kính $r=\dfrac{4 \sqrt{2}}{3}$

