Trả lời bởi giáo viên
Đáp án đúng: a
Đặt t=2x;x∈(1;3)⇒t=2x∈(2;8)
Xét hàm số y=t2−8t+3 trên (2;8) có:
y′=2t−8; y′=0⇔2t−8=0⇔t=4∈(2;8)
Bảng biến thiên:
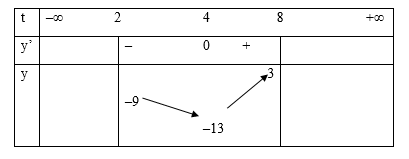
Căn cứ bảng biến thiên:
Phương trình 4x− 2x + 3+ 3 = m có đúng 2 nghiệm x∈(1;3)⇔−13<m<−9
Hướng dẫn giải:
- Đặt ẩn phụ đưa phương trình về bậc hai.
- Tìm điều kiện để bài toán phụ có nghiệm thỏa mãn điều kiện của ẩn phụ,

