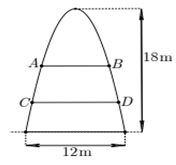
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số \(\dfrac{{AB}}{{CD}}\) bằng :
Trả lời bởi giáo viên
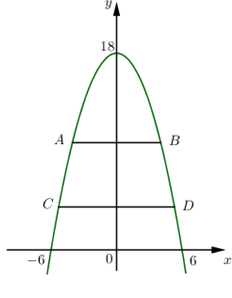
Gắn hệ trục tọa độ như hình vẽ :
Ta dễ dàng tìm được phương trình parabol là \(y = - \dfrac{1}{2}{x^2} + 18\)
Diện tích hình phẳng giới hạn bởi parabol và trục hoành là \(S = \int\limits_{ - 6}^6 {\left( { - \dfrac{1}{2}{x^2} + 18} \right)dx} = \left. {\left( { - \dfrac{{{x^3}}}{6} + 18x} \right)} \right|_{ - 6}^6 = 144.\)
Gọi \({x_A} = a \Rightarrow {y_A} = - \dfrac{1}{2}{a^2} + 18\)
\( \Rightarrow \) Phương trình đường thẳng AB : \(y = - \dfrac{1}{2}{a^2} + 18\)
và \({x_C} = c \Rightarrow {y_c} = - \dfrac{1}{2}{c^2} + 18\)
\( \Rightarrow \) Phương trình đường thẳng CD : \(y = - \dfrac{1}{2}{c^2} + 18\).
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng AB là:
$\begin{array}{l}{S_1} = \int\limits_{ - a}^a {\left( { - \dfrac{1}{2}{x^2} + 18 + \dfrac{1}{2}{a^2} - 18} \right)dx} = \int\limits_{ - a}^a {\left( { - \dfrac{1}{2}{x^2} + \dfrac{1}{2}{a^2}} \right)dx} = \left. {\left( { - \dfrac{{{x^3}}}{6} + \dfrac{{{a^2}}}{2}x} \right)} \right|_{ - a}^a = - \dfrac{{{a^3}}}{6} + \dfrac{{{a^3}}}{2} - \left( {\dfrac{{{a^3}}}{6} - \dfrac{{{a^3}}}{2}} \right) = \dfrac{{2{a^3}}}{3}.\\{S_1} = \dfrac{1}{3}S \Rightarrow \dfrac{2}{3}{a^3} = \dfrac{1}{3}.144 = 48 \Rightarrow a = 2\sqrt[3]{9} \Rightarrow AB = 2a = 4\sqrt[3]{9}.\end{array}$
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng CD là:
$\begin{array}{l}{S_2} = \int\limits_{ - c}^c {\left( { - \dfrac{1}{2}{x^2} + 18 + \dfrac{1}{2}{c^2} - 18} \right)dx} = \left. {\left( { - \dfrac{{{x^3}}}{6} + \dfrac{{{c^2}}}{2}x} \right)} \right|_{ - c}^c = - \dfrac{{{c^3}}}{6} + \dfrac{{{c^3}}}{2} - \left( {\dfrac{{{c^3}}}{6} - \dfrac{{{c^3}}}{2}} \right) = \dfrac{{2{c^3}}}{3}.\\{S_1} = \dfrac{2}{3}S \Rightarrow \dfrac{2}{3}{c^3} = \dfrac{2}{3}.144 = 96 \Rightarrow c = 2\sqrt[3]{{18}} \Rightarrow CD = 2c = 4\sqrt[3]{{18}}\\ \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{1}{{\sqrt[3]{2}}}\end{array}$
Hướng dẫn giải:
+) Gắn hệ trục tọa độ, tìm phương trình parabol. Tính diện tích S của hình phẳng giới hạn bởi parabol và trục hoành.
+) Gọi \({x_A} = a \Rightarrow AB = 2a\), tính diện tích hình S1 của phẳng giới hạn bởi parabol và đường thẳng AB.
+) Sử dụng giả thiết \({S_1} = \dfrac{1}{3}S\) tìm a và suy ra AB.
+) Tương tự tìm độ dài đoạn CD và tính tỉ số.