Câu hỏi:
2 năm trước
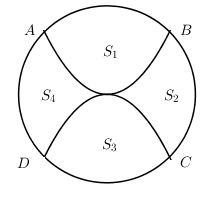
Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích \(S_1,S_3\) dùng để trồng hoa, phần diện tích \(S_2,S_4\) dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là \(150.000\) đồng/ \(m^2\), kinh phí trồng cỏ là \(100.000\) đồng/ \(m^2\). Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).
Trả lời bởi giáo viên
Đáp án đúng: c
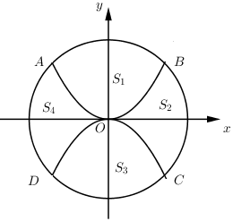
Gắn hệ trục tọa độ Oxy như hình vẽ, do ABCD là hình vuông cạnh 4m nên ta có \(A\left( { - 2;2} \right);B\left( {2;2} \right),C\left( {2; - 2} \right);D\left( { - 2; - 2} \right)\), từ đó ta dễ dàng viết được phương trình đường tròn là \({x^2} + {y^2} = 8\) và phương trình 2 parabol là \(y = \dfrac{1}{2}{x^2}\) và \(y = - \dfrac{1}{2}{x^2}\).
Ta có: S1 là diện tích hình phẳng giới hạn bởi đường tròn \({x^2} + {y^2} = 8\) và parabol (P): \(y = \dfrac{1}{2}{x^2}\)
\({S_1} = \int\limits_0^2 {\left( {\sqrt {8 - {x^2}} - \dfrac{1}{2}{x^2}} \right)dx} \) \(\Rightarrow {S_1} + {S_3} = 4\int\limits_0^2 {\left( {\sqrt {8 - {x^2}} - \dfrac{1}{2}{x^2}} \right)dx} = 15,23\left( {{m^2}} \right)\)
\({S_2} + {S_4} = \pi {\left( {2\sqrt 2 } \right)^2} - \left( {{S_1} + {S_3}} \right) = 9,90\left( {{m^2}} \right)\)
\( \Rightarrow \) Chi phí để trồng bồn hoa đó là: \(15,23.150 + 9,90.100 \approx 3270\) (nghìn đồng).
Hướng dẫn giải:
Gắn hệ trục tọa độ Oxy hợp lý, viết các phương trình đường tròn và phương trình parabol.
Ứng dụng tích phân để tính diện tích hình phẳng.
