Câu hỏi:
2 năm trước
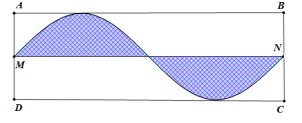
Ông A có một mảnh đất hình chữ nhật \(ABCD\) có \(AB = 2\pi \,\left( m \right),\,\,AD = 5\,\left( m \right)\). Ông muốn trồng hoa trên giải đất có giới hạn bởi hai đường trung bình $MN$ và đường hình $sin$ (như hình vẽ). Biết kinh phí trồng hoa là $100.000$ đồng $/{\rm{ }}{m^2}$ . Hỏi ông A cần bao nhiêu tiền để trồng hoa trên giải đất đó?
Trả lời bởi giáo viên
Đáp án đúng: a
Gắn hệ trục tọa độ $Oxy$ như hình vẽ:
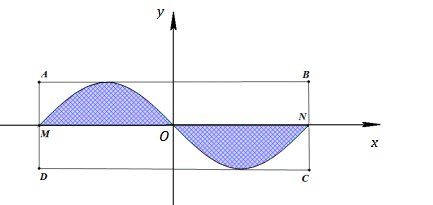
Dựa vào hình vẽ ta thấy đường $sin$ có chu kì bằng \(AB = 2\pi \) và biên độ bằng \(AM = \dfrac{1}{2}AD = \dfrac{5}{2}\) Đường hình $sin$ có phương trình \(y = - \dfrac{5}{2}\sin x\).
Đường thẳng $BC$ có phương trình \(x = \pi \).
Xét hình phẳng giới hạn bởi đồ thị hàm số \(y = - \dfrac{5}{2}\sin x\), trục $Ox$ , đường thẳng \(x = 0;\,\,x = \pi \) có $S = \int\limits_0^\pi {\left| { - \dfrac{5}{2}\sin x} \right|} dx = \dfrac{5}{2}\int\limits_0^\pi {\sin xdx} = - \left. {\dfrac{5}{2}\cos x} \right|_0^\pi = \dfrac{5}{2} + \dfrac{5}{2} = 5\,\,\left( m \right)$ .
\( \Rightarrow \) Diện tích giải đất ông A dùng để trồng hoa là \(2S = 10\,\,\left( {{m^2}} \right)\) , do đó kinh phí để trồng hoa là $1.000.000$ đồng.
Hướng dẫn giải:
- Gắn hệ trục tọa độ vào bài toán.
- Xác định hàm số đường hình sin.
- Xác định các đường giới hạn phần diện tích hình phẳng được tô xanh.
- Áp dụng công thức ứng dụng tích phân để tính diện tích hình phẳng.
