Cho tam giác \(ABC\) vuông tại \(A\), gọi \(H\) là hình chiếu của \(A\) lên \(BC\). Dựng hình bình hành \(ABCD\). Chọn kết luận không đúng:
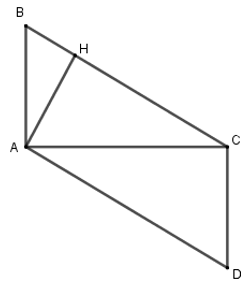
Xét \(\Delta ABC\) và \(\Delta CDA\) có:
\(AB = CD\left( {t/c} \right)\)
\(AC\) chung
\(\widehat {BAC} = \widehat {DCA} = {90^0}\)
Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c) hay D đúng.
Ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}AB.AC\) \( \Rightarrow AH.BC = AB.AC\) \( \Rightarrow \dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{BC}}\).
Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat {CAH} = \widehat {ABC}\) (cùng phụ góc \(\widehat C\))
\(\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{BC}}\)(cmt)
Suy ra \(\Delta ABC \backsim \Delta HAC\) (cạnh-góc-cạnh) nên A sai.
Ngoài ra, \(\Delta ADC = \Delta CBA\) và \(\Delta CBA \backsim \Delta CAH\) hay \(\Delta ADC \backsim \Delta CAH\) nên B đúng.
Từ \(\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{BC}} \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{BC}}\)
Xét \(\Delta ABH\) và \(\Delta CBA\) có:
\(\dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{BC}}\) (cmt)
Chung \(\widehat B\)
\( \Rightarrow \Delta ABH \backsim \Delta CBA\) (c-g-c)
Mà \(\Delta CBA = \Delta ADC\) nên \(\Delta ABH \backsim \Delta ADC\) hay C đúng.
Vậy chỉ có A sai.
Cho tam giác \(ABC\) có: \(AB = 9cm,AC = 12cm,BC = 7cm\). Chọn kết luận đúng.
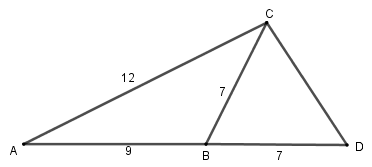
Ta có:
\(\dfrac{{AB}}{{AC}} = \dfrac{9}{{12}} = \dfrac{3}{4}\), \(\dfrac{{AC}}{{AD}} = \dfrac{{12}}{{9 + 7}} = \dfrac{3}{4}\)\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{AD}} = \dfrac{3}{4}\)
Xét tam giác \(ABC\) và \(ACD\) có:
Chung \(\widehat A\)
\(\dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{AD}}\)
\( \Rightarrow \Delta ABC \backsim \Delta ACD\left( {c.g.c} \right)\) \( \Rightarrow \widehat {ACB} = \widehat {ADC} = \widehat {BDC}\) (góc tương ứng) (1)
Mà \(\Delta BCD\) có: \(BC = BD\) nên là tam giác cân \( \Rightarrow \widehat {ADC} = \widehat {BCD}\).
Lại có: \(\widehat {ABC} = \widehat {BCD} + \widehat {BDC} = 2\widehat {BDC}\) (2)
Từ (1) và (2) suy ra: \(\widehat {ABC} = 2\widehat {ACB}\).
Hãy chọn câu đúng. Nếu $\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì:
$\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì $\Delta ABC$ đồng dạng với $\Delta EDF$
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
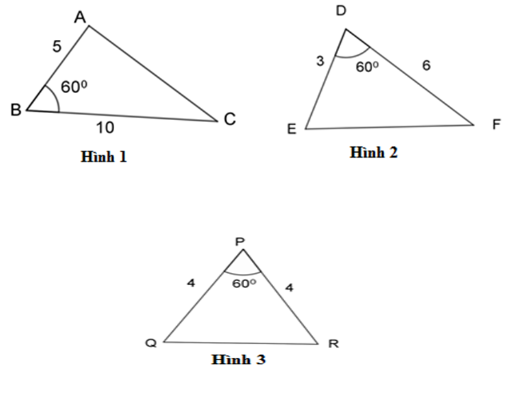
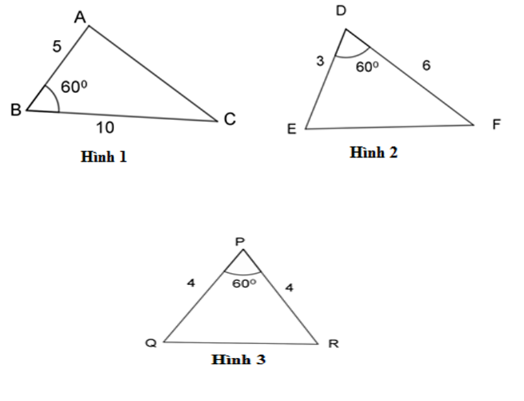
Có: \(\dfrac{{BA}}{{BC}} = \dfrac{5}{{10}} = \dfrac{1}{2},\;\dfrac{{DE}}{{DF}} = \dfrac{3}{6} = \dfrac{1}{2},\;\dfrac{{PQ}}{{PR}} = \dfrac{4}{4} = 1 \Rightarrow \dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}} = \dfrac{1}{2}.\)
Xét \(\Delta ABC\) và $\Delta EDF$ ta có:
$\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}\,\,\left( {cmt} \right) $$\Leftrightarrow \dfrac{{DE}}{{BA}} = \dfrac{{DF}}{{BC}}$
$\widehat B = \widehat D = {60^0}\;(gt)$
$\Rightarrow \Delta ABC\backsim \Delta EDF\,\,\,\left( {c - g - c} \right).$
Cho \(\Delta ABC\), lấy 2 điểm $D$ và $E$ lần lượt nằm bên cạnh $AB$ và $AC$ sao cho \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\). Kết luận nào sai?
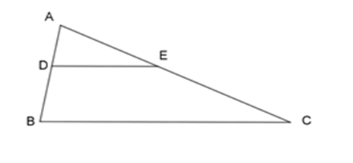
Xét $\Delta ADE$ và $\Delta ABC$ ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) (theo gt)
$\widehat A$ chung.
$ \Rightarrow \Delta ADE\backsim\Delta ABC$ (c – g – c)
$ \Rightarrow \widehat {ADE} = \widehat {ABC}$ (cặp góc tương ứng)
$ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}} \Rightarrow DE{\rm{//}}BC$ (định lý Talet đảo)
Cho hình vẽ dưới đây, tính giá trị của $x$ ?
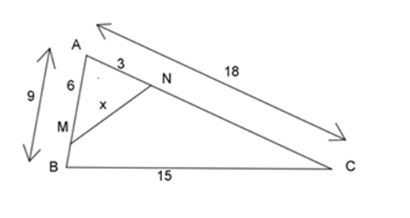
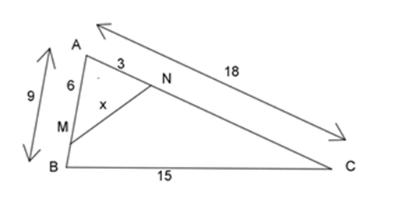
Ta có: \(\)
\(\dfrac{{AN}}{{AB}} = \dfrac{3}{9} = \dfrac{1}{3}\), \(\dfrac{{AM}}{{AC}} = \dfrac{6}{{18}} = \dfrac{1}{3}\)\( \Rightarrow \dfrac{{AN}}{{AB}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3}\)
Xét \(\Delta ANM\) và \(\Delta ABC\) có:
\(\dfrac{{AN}}{{AB}} = \dfrac{{AM}}{{AC}}\)(chứng minh trên)
\(\widehat A\;chung\)
\( \Rightarrow \Delta ANM\backsim\Delta ABC\) (c – g – c)
\(\begin{array}{l} \Rightarrow \dfrac{{AN}}{{AB}} = \dfrac{{AM}}{{AC}} = \dfrac{{MN}}{{CB}} = \dfrac{1}{3}\\ \Rightarrow \dfrac{x}{{15}} = \dfrac{1}{3} \Rightarrow x = \dfrac{{15}}{3} = 5\end{array}\)
Với \(AB{\rm{//}}CD\) thì giá trị của \(x\) trong hình vẽ dưới đây là
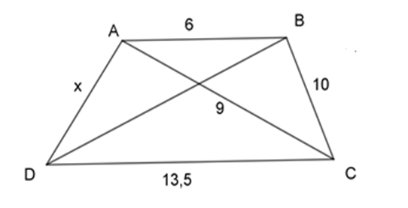
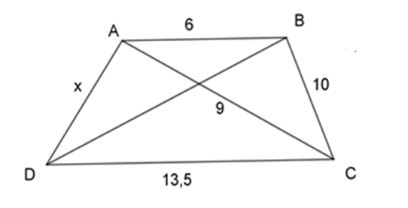
Ta có:
\(\dfrac{{AB}}{{AC}} = \dfrac{6}{9} = \dfrac{2}{3}\), \(\dfrac{{AC}}{{CD}} = \dfrac{9}{{13,5}} = \dfrac{2}{3}\) \( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{CD}} = \dfrac{2}{3}\)
Xét \(\Delta ABC\) và \(\Delta CAD\) có:
\(\dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{CD}}\) (chứng minh trên)
\(\widehat {BAC} = \widehat {ACD}\) (cặp góc so le trong)
\( \Rightarrow \Delta ABC\backsim\Delta CAD\) (c – g – c)
\(\begin{array}{l} \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{CA}}{{CD}} = \dfrac{{BC}}{{AD}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{10}}{x} = \dfrac{2}{3} \Rightarrow x = \dfrac{{10.3}}{2} = 15\end{array}\)
Cho tam giác ABC có \(AB = 12cm,\;AC = 18cm,\;BC = 27cm.\) Điểm $D$ thuộc cạnh $BC$ sao cho
$CD = 12\,cm$ . Tính độ dài $AD$ .
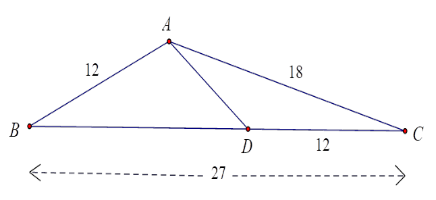
Ta có
\(\begin{array}{l}\dfrac{{AC}}{{DC}} = \dfrac{{18}}{{12}} = \dfrac{3}{2};\,\dfrac{{CB}}{{CA}} = \dfrac{{27}}{{18}} = \dfrac{3}{2}\\ \Rightarrow \dfrac{{CA}}{{CD}} = \dfrac{{CB}}{{CA}}\end{array}\)
Xét \(\Delta ACB\) và \(\Delta DCA\) có \(\widehat C\) chung và \(\dfrac{{CA}}{{CD}} = \dfrac{{CB}}{{CA}}\,\left( {cmt} \right)\)
Nên $\Delta ACB$ \(\backsim\) $\Delta DCA$ (c.g.c)
\(\begin{array}{l} \Rightarrow \dfrac{{AC}}{{DC}} = \dfrac{{AB}}{{DA}} \Leftrightarrow \dfrac{3}{2} = \dfrac{{12}}{{DA}}\\ \Rightarrow DA = \dfrac{{2.12}}{3} = 8\,cm\end{array}\)
Cho hình thang vuông $ABCD$ \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có $AB = 16\,cm,CD = 25\,cm,BD = 20\,cm$ .
Tam giác \(ABD\) đồng dạng với tam giác nào dưới đây?
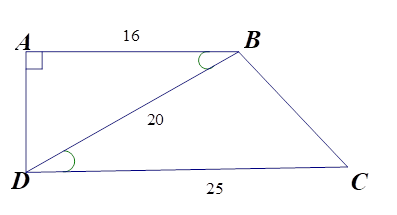
\(\Delta ABD\) và \(\Delta BDC\) có \(\widehat {ABD} = \widehat {BDC}\) (hai góc ở vị trí so le trong bằng nhau do\(AB{\rm{//CD}}\));
Và \(\dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}}\) (vì \(\dfrac{{16}}{{20}} = \dfrac{{20}}{{25}}\)).
Do đó \(\Delta ABD \backsim \Delta BDC\) (c.g.c).
Cho hình thang vuông $ABCD$ \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có $AB = 16\,cm,CD = 25\,cm,BD = 20\,cm$ .
Độ dài cạnh \(BC\) là
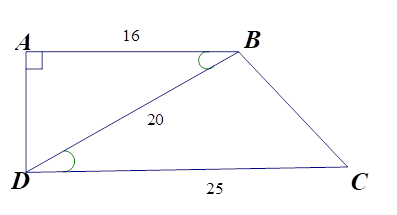
Vì \(\Delta ABD \backsim \Delta BDC\) (cmt) nên \(\widehat A = \widehat {DBC}\).
Ta có \(\widehat A = {90^0}\) nên \(\widehat {DBC} = {90^0}\). Theo định lí Py-ta-go, ta có
\(B{C^2} = C{D^2} - B{D^2} = {25^2} - {20^2} = {15^2}.\) Vậy \(BC = 15cm.\)
Cho tam giác ABC có \(AB = 8cm,\;AC = 16cm.\) Điểm $D$ thuộc cạnh $AB$ sao cho
$BD = 2cm$ . Điểm $E$ thuộc cạnh $AC$ sao cho $CE = 13cm$ .
Chọn câu đúng.
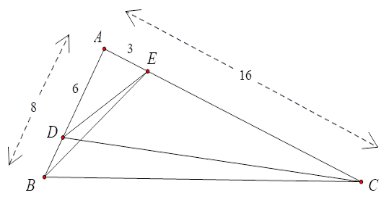
Ta có
\(\begin{array}{l}\dfrac{{AE}}{{AB}} = \dfrac{3}{8};\,\dfrac{{AD}}{{AC}} = \dfrac{6}{{16}} = \dfrac{3}{8}\\ \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}}\end{array}\)
Xét \(\Delta AED\) và \(\Delta ABC\) có \(\widehat A\) chung và \(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}}\,\left( {cmt} \right)\)
Nên \(\Delta AED\)\(\backsim\)\(\Delta ABC\) (c.g.c)
Cho tam giác ABC có \(AB = 8cm,\;AC = 16cm.\) Điểm $D$ thuộc cạnh $AB$ sao cho
$BD = 2cm$ . Điểm $E$ thuộc cạnh $AC$ sao cho $CE = 13cm$ .
Chọn câu sai.
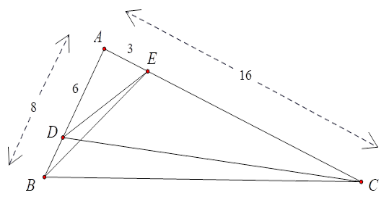
+ Xét \(\Delta ABE\) và \(\Delta ACD\) có \(\widehat A\) chung và $\dfrac{{AE}}{{AD}} = \dfrac{{AB}}{{AC}}\left( { = \dfrac{1}{2}} \right)$ nên \(\Delta {\rm A}{\rm B}{\rm E}\backsim\Delta ACD\,\left( {c - g - c} \right)\) suy ra \(\widehat {ABE} = \widehat {ACD}\) (hai góc tương ứng) và \(\dfrac{{AE}}{{AD}} = \dfrac{{BE}}{{CD}} \Rightarrow AE.CD = AD.BE\) .
+ \(\Delta AED\)\(\backsim\)\(\Delta ABC\) (cmt) nên \(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}} \Leftrightarrow AE.AC = AB.AD\).
Nên A, C, D đúng, B sai.
Cho tam giác nhọn ABC có \(\widehat C = {40^0}\). Vẽ hình bình hành $ABCD$ . Gọi $AH,AK$ theo thứ tự là các đường cao của các tam giác $ABC,ACD$ . Tính số đo $\widehat {AKH}$ .
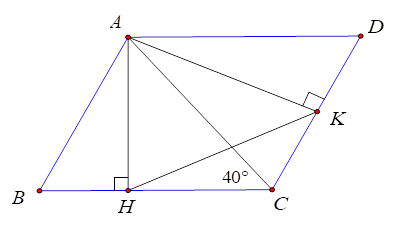
Vì $AD.AH = AB.AK$ \(( = {S_{ABCD}})\) nên \(\dfrac{{AH}}{{AK}} = \dfrac{{AB}}{{AD}} = \dfrac{{AB}}{{BC}}.\)
Ta lại có \(AB{\rm{//}}CD\,\)( vì $ABCD$ là hình bình hành) mà \(AK \bot DC \Rightarrow AK \bot AB \)\(\Rightarrow \widehat {BAK} = 90^\circ. \)
Từ đó \(\widehat {HAK} = \widehat {ABC}\) (cùng phụ với \(\widehat {BAH}\) )
Nên \(\Delta AKH\backsim\Delta BCA\)(c.g.c) \( \Rightarrow \widehat {AKH} = \widehat {ACB} = 40^\circ \) .
Cho tam giác $ABC$ có $AB = 9\,cm,AC = 16\,cm,BC = 20\,cm$ . Khi đó
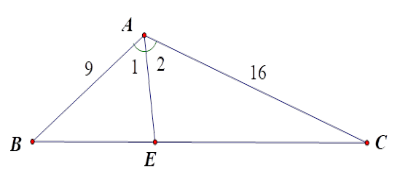
Kẻ đường phân giác $AE$ của \(\widehat {BAC}\) . Theo tính chất đường phân giác, ta có:
$\dfrac{{BE}}{{EC}} = \dfrac{{AB}}{{AC}} = \dfrac{9}{{16}}$ nên
$\dfrac{{BE + EC}}{{EC}} = \dfrac{{9 + 16}}{{16}}$ hay $\dfrac{{20}}{{EC}} = \dfrac{{25}}{{16}}.$
Suy ra $EC = 12,8\,cm$ .
Xét \(\Delta ACB\) và \(\Delta ECA\) có
\(\widehat C\) là góc chung;
$\dfrac{{AC}}{{CB}} = \dfrac{{EC}}{{CA}}$ (vì $\dfrac{{16}}{{20}} = \dfrac{{12,8}}{{16}}$).
Do đó \(\Delta ACB \backsim \Delta ECA\) (c.g.c) suy ra \(\widehat B = {\widehat A_2}\), tức là \(\widehat B = \widehat {\dfrac{A}{2}}\).

