Câu hỏi:
2 năm trước
Cho hình thang vuông $ABCD$ \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có $AB = 16\,cm,CD = 25\,cm,BD = 20\,cm$ .
Độ dài cạnh \(BC\) là
Trả lời bởi giáo viên
Đáp án đúng: c
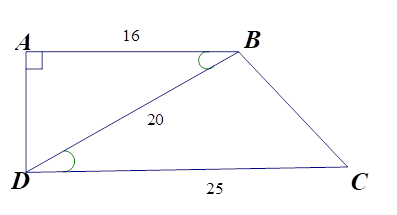
Vì \(\Delta ABD \backsim \Delta BDC\) (cmt) nên \(\widehat A = \widehat {DBC}\).
Ta có \(\widehat A = {90^0}\) nên \(\widehat {DBC} = {90^0}\). Theo định lí Py-ta-go, ta có
\(B{C^2} = C{D^2} - B{D^2} = {25^2} - {20^2} = {15^2}.\) Vậy \(BC = 15cm.\)
Hướng dẫn giải:
Từ \(\Delta ABD \backsim \Delta BDC\) ta suy ra \(\widehat {DBC}\) vuông nên áp dụng định lý Pytago để tính cạnh \(BC\) .
Giải thích thêm:
- Học sinh cần đổi giá trị các đoạn thẳng về cùng một đơn vị đo (nếu có).
- Học sinh cần viết các cặp đoạn thẳng tỉ lệ và cặp tam giác đồng dạng theo đúng thứ tự đỉnh tương ứng của 2 tam giác.
- Học sinh cần chú ý trong kĩ năng đại số biến đổi tỉ lệ thức về dạng biểu thức để tính độ dài, tránh mắc sai lầm trong tính toán.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
