Trả lời bởi giáo viên
Đáp án đúng: b
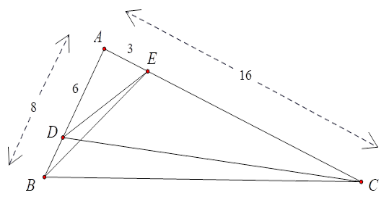
+ Xét \(\Delta ABE\) và \(\Delta ACD\) có \(\widehat A\) chung và $\dfrac{{AE}}{{AD}} = \dfrac{{AB}}{{AC}}\left( { = \dfrac{1}{2}} \right)$ nên \(\Delta {\rm A}{\rm B}{\rm E}\backsim\Delta ACD\,\left( {c - g - c} \right)\) suy ra \(\widehat {ABE} = \widehat {ACD}\) (hai góc tương ứng) và \(\dfrac{{AE}}{{AD}} = \dfrac{{BE}}{{CD}} \Rightarrow AE.CD = AD.BE\) .
+ \(\Delta AED\)\(\backsim\)\(\Delta ABC\) (cmt) nên \(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}} \Leftrightarrow AE.AC = AB.AD\).
Nên A, C, D đúng, B sai.
Hướng dẫn giải:
Bước 1: Chứng minh \(\Delta {\rm A}{\rm B}{\rm E}\backsim\Delta ACD\) (cạnh-góc-cạnh) từ đó suy ra cặp góc bằng nhau và hệ thức giữa các cạnh.
Bước 2: Từ \(\Delta AED\)\(\backsim\)\(\Delta ABC\) suy ra tỉ lệ cạnh từ đó có hệ thức đúng giữa các cạnh.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
