Câu hỏi:
2 năm trước
Cho hình thang vuông $ABCD$ \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có $AB = 16\,cm,CD = 25\,cm,BD = 20\,cm$ .
Tam giác \(ABD\) đồng dạng với tam giác nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: a
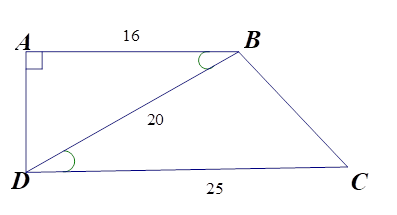
\(\Delta ABD\) và \(\Delta BDC\) có \(\widehat {ABD} = \widehat {BDC}\) (hai góc ở vị trí so le trong bằng nhau do\(AB{\rm{//CD}}\));
Và \(\dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}}\) (vì \(\dfrac{{16}}{{20}} = \dfrac{{20}}{{25}}\)).
Do đó \(\Delta ABD \backsim \Delta BDC\) (c.g.c).
Hướng dẫn giải:
- Xét tỉ số độ dài của các cạnh tương ứng của 2 tam giác.
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
