Cho tam giác \(ABC\) vuông tại \(A\), gọi \(H\) là hình chiếu của \(A\) lên \(BC\). Dựng hình bình hành \(ABCD\). Chọn kết luận không đúng:

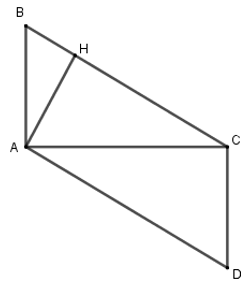
Xét \(\Delta ABC\) và \(\Delta CDA\) có:

\(AB = CD\left( {t/c} \right)\)

\(AC\) chung

\(\widehat {BAC} = \widehat {DCA} = {90^0}\)

Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c) hay D đúng.

Ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}AB.AC\) \( \Rightarrow AH.BC = AB.AC\) \( \Rightarrow \dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{BC}}\).

Xét \(\Delta ABC\) và \(\Delta HAC\) có:

\(\widehat {CAH} = \widehat {ABC}\) (cùng phụ góc \(\widehat C\))

\(\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{BC}}\)(cmt)

Suy ra \(\Delta ABC \backsim \Delta HAC\) (cạnh-góc-cạnh) nên A sai.

Ngoài ra, \(\Delta ADC = \Delta CBA\) và \(\Delta CBA \backsim \Delta CAH\) hay \(\Delta ADC \backsim \Delta CAH\) nên B đúng.

Từ \(\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{BC}} \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{BC}}\)

Xét \(\Delta ABH\) và \(\Delta CBA\) có:

\(\dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{BC}}\) (cmt)

Chung \(\widehat B\)

\( \Rightarrow \Delta ABH \backsim \Delta CBA\) (c-g-c)

Mà \(\Delta CBA = \Delta ADC\) nên \(\Delta ABH \backsim \Delta ADC\) hay C đúng.

Vậy chỉ có A sai.