Cho tam giác $ABC$ có: $AB = 9cm,AC = 12cm,BC = 7cm$. Chọn kết luận đúng.

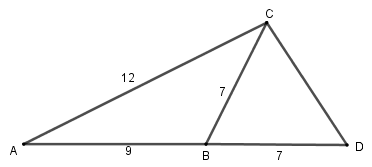
Ta có:

$\dfrac{{AB}}{{AC}} = \dfrac{9}{{12}} = \dfrac{3}{4}$, $\dfrac{{AC}}{{AD}} = \dfrac{{12}}{{9 + 7}} = \dfrac{3}{4}$$\Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{AD}} = \dfrac{3}{4}$

Xét tam giác $ABC$ và $ACD$ có:

Chung $\widehat A$

$\dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{AD}}$

$\Rightarrow \Delta ABC \backsim \Delta ACD\left( {c.g.c} \right)$ $\Rightarrow \widehat {ACB} = \widehat {ADC} = \widehat {BDC}$ (góc tương ứng) (1)

Mà $\Delta BCD$ có: $BC = BD$ nên là tam giác cân $\Rightarrow \widehat {ADC} = \widehat {BCD}$.

Lại có: $\widehat {ABC} = \widehat {BCD} + \widehat {BDC} = 2\widehat {BDC}$  (2)

Từ (1) và (2) suy ra: $\widehat {ABC} = 2\widehat {ACB}$.