Đối xứng tâm

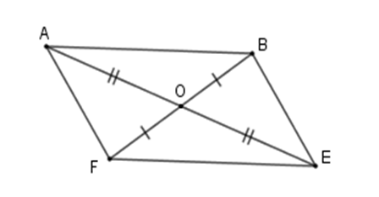
Hình bình hành \(ABCD\) có \(OA = OE;\,OB = OF\)  nên

+ \(E\) và \(A\) đối xứng nhau qua \(O\).

+ \(B\) và \(F\) đối xứng nhau qua \(O\).

+ \(AB\) và $EF$ đối xứng nhau qua \(O\).

Nhưng \(E\) và \(F\) không đối xứng nhau qua \(O\)  vì \(OE \ne OF;\,O\) không thuộc \(EF\) .

Vậy có \(3\) khẳng định đúng.

Vì tam giác \(ABC\) đối xứng với tam giác \(A'B'C'\) qua \(O\) nên \(\Delta ABC = \Delta A'B'C'\) \( \Rightarrow AB = A'B';\,AC = A'C';\,BC = B'C'\)

Nên \(AB + AC + BC = A'B' + A'C' + B'C'\) \( \Rightarrow {P_{ABC}} = {P_{A'B'C'}}\)

Do đó chu vi tam giác \(ABC\) là \({P_{ABC}} = 32\,cm\) .

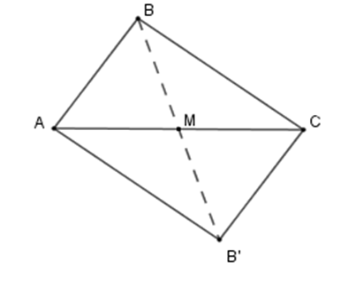
Lấy \(M\) là trung điểm \(AC\) khi đó \(A,\,C\) đối xứng nhau qua \(M\) . Vẽ \(B'\) đối xứng với \(B\) qua \(O\) . Khi đó tam giác \(B'AC\) đối xứng với tam giác $ABC$ qua \(M\) . Tứ giác tạo thành là \(ABCB'\) .

Vì tam giác \(B'AC\) đối xứng với tam giác $BCA$ qua \(M\) nên \(AB' = BC = 15\,cm;\,B'C= AB = 12\,cm\)

Chu vi tứ giác \(ABCB'\) là $AB + AC + CB' + AB' $$= 12 + 15 + 12 + 15 = 54\,cm$ .

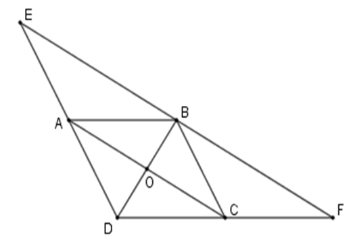
Gọi \(O\) là giao điểm hai đường chéo của hình bình hành \(ABCD\) khi đó \(OA = OC;\,OB = OD\)

Xét tam giác \(DBE\) ta có \(OA\) là đường trung bình nên \(OA{\rm{//}}EB;\,OA = \dfrac{1}{2}EB \Rightarrow AC{\rm{//}}EB;\,OA = \dfrac{1}{2}EB\)  \(\left( 1 \right)\)

Tương tự \(OC\) là đường trung bình của tam giác $BDF $ \(\Rightarrow OC{\rm{//}}BF;\,OC = \dfrac{1}{2}FB \Rightarrow AC{\rm{//}}BF;\,OC = \dfrac{1}{2}FB\) \(\left( 2 \right)\)

Từ \(\left( 1 \right);\,\left( 2 \right) \Rightarrow E;\,B;F\) thẳng hàng và \(EB = BF\) (vì \(OA = OC\) ) hay \(E\) đối xứng với \(F\) qua điểm \(B\) .

Để \(E\) đối xứng với \(F\) qua đường thẳng \(BD\)  ta cần thêm điều kiện \(EF \bot BD\).

Mà \(AC\) là đường trung bình của tam giác \(DEF\) nên \(AC{\rm{//}}\,EF\) suy ra \(BD \bot AC\) .

Vậy hình bình hành $ABCD$ có thêm điều kiện hai đường chéo vuông góc thì \(E\) đối xứng với \(F\) qua đường thẳng \(DB\).

Gọi tam giác \(A'CB\) đối xứng với tam giác \(ABC\) qua trung điểm cạnh \(BC\) . Khi đó \(\Delta ABC = \Delta A'CB\)

Nên \({S_{ABC}} = {S_{A'BC}}\) .

Ta có \({S_{ABC}} = \dfrac{1}{2}AH.BC \)\(= \dfrac{1}{2}.3.18 = 27\,c{m^2}\) nên ${S_{A'BC}} = 27\,c{m^2}$ .

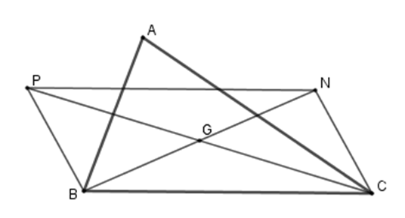
Vì $N,P$ theo thứ tự là các điểm đối xứng của $B,C$ qua trọng tâm$G$ nên \(G\) là trung điểm của \(CP;\,BN\) .

Xét tứ giác \(BPNC\) có hai đường chéo \(CP\) và \(BN\)  giao nhau tại trung điểm mỗi đường nên \(BPNC\) là hình bình hành (dhnb).

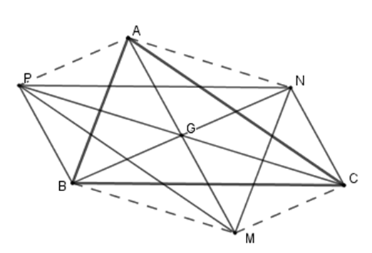
Tương tự câu a) ta có  tứ giác \(MNAB\) là hình bình hành (do hai đường chéo giao nhau tại trung điểm \(G\) mỗi đường) suy ra \(MN = AB\)  \(\left( 1 \right)\) (tính chất hình bình hành).

Và tứ giác \(PMCA\) là hình bình hành (do hai đường chéo giao nhau tại trung điểm \(G\) mỗi đường) suy ra \(PM = AC\) \(\left( 2 \right)\)  (tính chất hình bình hành).

Lại có \(PN = BC\) \(\left( 3 \right)\) (do \(BPNC\) là hình bình hành (cmt))

Từ \(\left( 1 \right);\,\left( 2 \right);\,\left( 3 \right)\) suy ra \(\Delta ABC = \Delta MNP\,\left( {c - c - c} \right)\) mà tam giác \(ABC\) không là tam giác đều (gt) nên \(\Delta MNP\) không là tam giác đều.

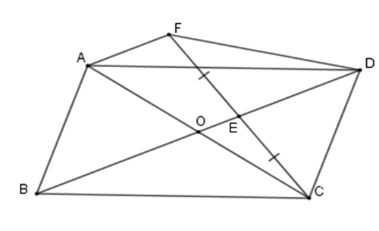
+ Xét tam giác \(CAF\) có \(E\) là trung điểm của \(CF\) ( do $F$ là điểm đối xứng của điểm $C$ qua$E$); \(O\) là trung điểm \(AC\) (do \(O\) là tâm đối xứng của hình bình hành\(ABCD\) ) nên \(OE\) là đường trung bình của tam giác \(CAF \Rightarrow OE = \dfrac{1}{2}AF;\,OE{\rm{//}}AF\)  suy ra \(OD\,{\rm{//}}\,AF \Rightarrow ODFA\) là hình thang.

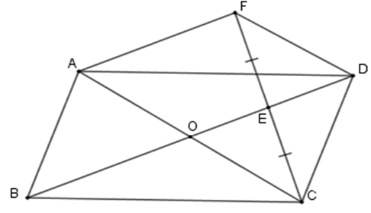
Để hình thang \(ODFA\) là hình bình hành thì ta cần \(OD = AF\) mà \(OE = \dfrac{1}{2}AF\) (cmt) nên \(OE = \dfrac{1}{2}OD\)

Hay \(E\) là trung điểm của \(OD\) .

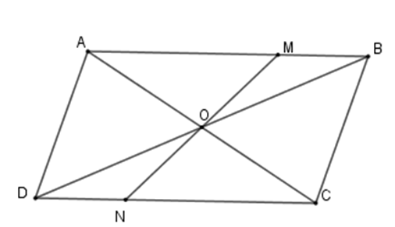
Xét tam giác \(\Delta OMB\) và \(\Delta OND\) có

+ \(\widehat {MOB} = \widehat {NOD}\) (đối đỉnh)

+ \(OB = OD\) (tính chất hình bình hành)

+ \(\widehat {MBO} = \widehat {NDO}\)  (so le trong)

Nên \(\Delta OMB = \Delta OND\,\left( {g - c - g} \right) \Rightarrow OM = ON\) (hai cạnh tương ứng)

Suy ra điểm $M$ đối xứng với điểm $N$ qua $O$.