Hãy chọn câu đúng. Cho hình bình hành \(ABCD\). Lấy điểm \(E\) thuộc tia đối của tia \(AD\) sao cho \(AD = AE\), lấy \(F\) thuộc tia đối của tia \(CD\) sao cho \(CD = CF\). Hình bình hành \(ABCD\) có thêm  điều kiện gì để \(E\) đối xứng với \(F\) qua đường thẳng \(DB\) ?

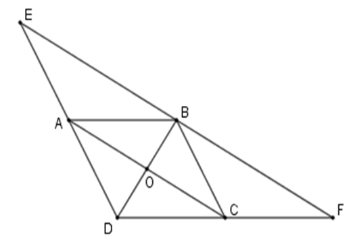
Gọi \(O\) là giao điểm hai đường chéo của hình bình hành \(ABCD\) khi đó \(OA = OC;\,OB = OD\)

Xét tam giác \(DBE\) ta có \(OA\) là đường trung bình nên \(OA{\rm{//}}EB;\,OA = \dfrac{1}{2}EB \Rightarrow AC{\rm{//}}EB;\,OA = \dfrac{1}{2}EB\)  \(\left( 1 \right)\)

Tương tự \(OC\) là đường trung bình của tam giác $BDF $ \(\Rightarrow OC{\rm{//}}BF;\,OC = \dfrac{1}{2}FB \Rightarrow AC{\rm{//}}BF;\,OC = \dfrac{1}{2}FB\) \(\left( 2 \right)\)

Từ \(\left( 1 \right);\,\left( 2 \right) \Rightarrow E;\,B;F\) thẳng hàng và \(EB = BF\) (vì \(OA = OC\) ) hay \(E\) đối xứng với \(F\) qua điểm \(B\) .

Để \(E\) đối xứng với \(F\) qua đường thẳng \(BD\)  ta cần thêm điều kiện \(EF \bot BD\).

Mà \(AC\) là đường trung bình của tam giác \(DEF\) nên \(AC{\rm{//}}\,EF\) suy ra \(BD \bot AC\) .

Vậy hình bình hành $ABCD$ có thêm điều kiện hai đường chéo vuông góc thì \(E\) đối xứng với \(F\) qua đường thẳng \(DB\).