Trả lời bởi giáo viên
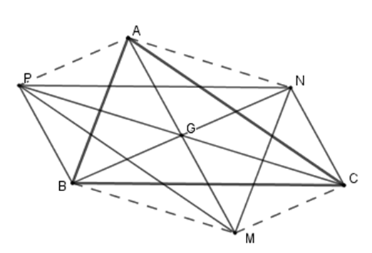
Tương tự câu a) ta có tứ giác \(MNAB\) là hình bình hành (do hai đường chéo giao nhau tại trung điểm \(G\) mỗi đường) suy ra \(MN = AB\) \(\left( 1 \right)\) (tính chất hình bình hành).
Và tứ giác \(PMCA\) là hình bình hành (do hai đường chéo giao nhau tại trung điểm \(G\) mỗi đường) suy ra \(PM = AC\) \(\left( 2 \right)\) (tính chất hình bình hành).
Lại có \(PN = BC\) \(\left( 3 \right)\) (do \(BPNC\) là hình bình hành (cmt))
Từ \(\left( 1 \right);\,\left( 2 \right);\,\left( 3 \right)\) suy ra \(\Delta ABC = \Delta MNP\,\left( {c - c - c} \right)\) mà tam giác \(ABC\) không là tam giác đều (gt) nên \(\Delta MNP\) không là tam giác đều.
Hướng dẫn giải:
Bước 1: Chứng minh tương tự câu a) ta có \(MNAB;\,PMCA\) là hình bình hành.
Bước 2: Sử dụng tính chất hình bình hành để suy ra các cặp cạnh bằng nhau. Từ đó suy ra các tam giác bằng nhau.

