Câu hỏi:
2 năm trước
Cho tam giác $ABC$ , trọng tâm $G$ . Gọi $N,P$ theo thứ tự là các điểm đối xứng của $B,C$ qua trọng tâm $G$ .
Tứ giác \(BPNC\) là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: b
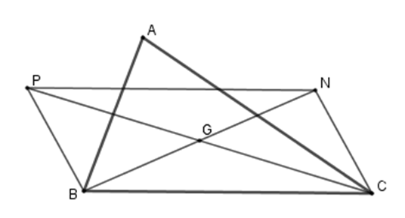
Vì $N,P$ theo thứ tự là các điểm đối xứng của $B,C$ qua trọng tâm$G$ nên \(G\) là trung điểm của \(CP;\,BN\) .
Xét tứ giác \(BPNC\) có hai đường chéo \(CP\) và \(BN\) giao nhau tại trung điểm mỗi đường nên \(BPNC\) là hình bình hành (dhnb).
Hướng dẫn giải:
Sử dụng định nghĩa điểm đối xứng để suy ra tứ giác \(BPNC\) có hai đường chéo giao nhau tại trung điểm mỗi đường nên \(BPNC\) là hình bình hành.

