Câu hỏi:
3 năm trước
Cho hình bình hành $ABCD$ có tâm đối xứng là $O$ , $E$ là điểm bất kỳ trên đoạn $OD.$ Gọi $F$ là điểm đối xứng của điểm $C$ qua $E$ .
Xác định vị trí điểm $E$ trên $OD$ để hình thang $ODFA$ là hình bình hành.
Trả lời bởi giáo viên
Đáp án đúng: b
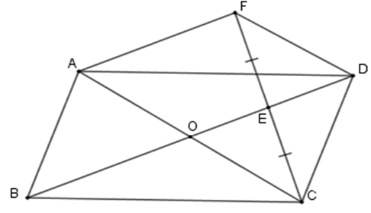
Để hình thang \(ODFA\) là hình bình hành thì ta cần \(OD = AF\) mà \(OE = \dfrac{1}{2}AF\) (cmt) nên \(OE = \dfrac{1}{2}OD\)
Hay \(E\) là trung điểm của \(OD\) .
Hướng dẫn giải:
Để hình thang \(ODFA\) là hình bình hành thì ta cần \(OD = AF\) từ đó suy ra vị trí điểm \(E\) trên \(OD\) .

