Câu hỏi:
2 năm trước
Cho hình bình hành $ABCD$ , $O$ là giao điểm của hai đường chéo. Một đường thẳng đi qua $O$ cắt các cạnh $AB$ và $CD$ theo thứ tự ở $M$ và $N$ . Chọn khẳng định đúng.
Trả lời bởi giáo viên
Đáp án đúng: a
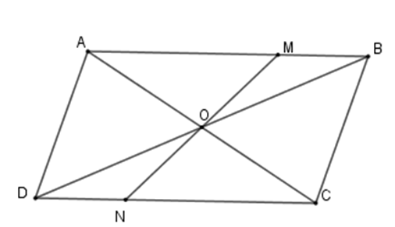
Xét tam giác \(\Delta OMB\) và \(\Delta OND\) có
+ \(\widehat {MOB} = \widehat {NOD}\) (đối đỉnh)
+ \(OB = OD\) (tính chất hình bình hành)
+ \(\widehat {MBO} = \widehat {NDO}\) (so le trong)
Nên \(\Delta OMB = \Delta OND\,\left( {g - c - g} \right) \Rightarrow OM = ON\) (hai cạnh tương ứng)
Suy ra điểm $M$ đối xứng với điểm $N$ qua $O$.
Hướng dẫn giải:
Từ hai tam giác bằng nhau suy ra \(O\) là trung điểm \(MN\) nên $M$ đối xứng với điểm $N$ qua $O$

