Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(HB = 3,5\)cm và \(HC = 9\)cm. Điểm \(E\) thuộc đoạn thẳng \(HC\) sao cho đường thẳng đi qua \(E\) và vuông góc với \(BC\) chia tam giác \(ABC\) thành hai phần có diện tích bằng nhau. Tính \(CE\).
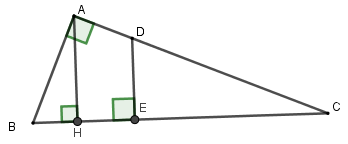
Gọi \(D\) là giao điểm của \(AC\) và đường vuông góc với \(BC\) tại \(E\).
Xét \(\Delta AHC\) và \(\Delta BAC\) có:
\(\widehat C\) chung và \(\widehat {AHC} = \widehat {BAC} = 90^\circ \) nên \(\Delta AHC\backsim\Delta BAC\,\left( {g - g} \right)\)
Ta có: \({S_{DEC}} = \dfrac{1}{2}{S_{ABC}}\) (1), \({S_{AHC}}:{S_{BAC}} = \dfrac{{HC}}{{BC}} = \dfrac{9}{{9 + 3,5}} = \dfrac{{18}}{{25}}\) (2).
Từ (1) và (2) suy ra \({S_{DEC}}:{S_{AHC}} = \dfrac{1}{2}:\dfrac{{18}}{{25}} = \dfrac{{25}}{{36}} = {\left( {\dfrac{5}{6}} \right)^2}\) (3).
Vì \(DE{\rm{//}}AH\) (cùng vuông với \(BC\)) suy ra \(\Delta DEC\backsim\Delta AHC\) nên \({S_{DEC}}:{S_{AHC}} = {\left( {\dfrac{{EC}}{{HC}}} \right)^2}\) (4).
Từ (3) và (4) suy ra \(\dfrac{{EC}}{{HC}} = \dfrac{5}{6}\) tức là \(\dfrac{{EC}}{9} = \dfrac{5}{6} \Rightarrow EC = 7,5\,{\rm{cm}}\).
Tích \(HB.HC\) bằng
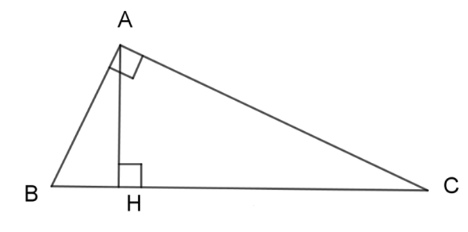
Ta có: \(\widehat {HAB} + \widehat {HAC} = \widehat {BAC} = {90^0}\)
Mà: \(\widehat {HBA} + \widehat {HAB} = {90^0}\) (2 góc phụ nhau)
\( \Rightarrow \widehat {HAC} = \widehat {HBA}\)
Xét 2 tam giác vuông AHB và CHA ta có: \(\widehat {HAC} = \widehat {HBA}\) (cmt)
\( \Rightarrow \Delta AHB\backsim\Delta CHA\;(g - g)\)
\( \Rightarrow \dfrac{{AH}}{{CH}} = \dfrac{{HB}}{{HA}} \Leftrightarrow A{H^2} = HB.HC\)
Tính độ dài các đoạn $AD,DC$ lần lượt là
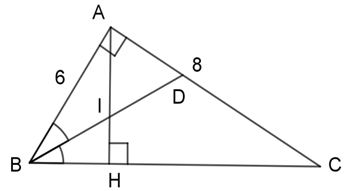
+ Áp dụng định lý Pitago trong tam giác vuông $ABC$ ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {6^2} + {8^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 100\\ \Rightarrow BC = 10\;cm\end{array}\)
+ Vì $BD$ là đường phân giác của tam giác $ABC$ nên áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}}\\ \Leftrightarrow \dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CA - AD}}\)\( \Leftrightarrow \dfrac{6}{{AD}} = \dfrac{{10}}{{8 - AD}}\\ \Rightarrow AD = 3\;cm\\ \Rightarrow DC = AC - AD \)\(= 8 - 3 = 5\;cm\)
Cho các mệnh đề sau. Chọn câu đúng.
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Vậy (I) đúng, (II) sai.
Cho hình vẽ dưới đây với \(\widehat {BAH} = \widehat {ACH}\) .
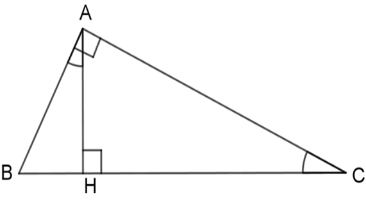
Khi đó các mệnh đề
(I) \(\Delta AHB\backsim\Delta CHA\;(g - g)\)
(II) \(\Delta AHC\backsim\Delta BAC\;(g - g)\)
Xét $2$ tam giác vuông $AHB$ và $CHA$ có: \(\widehat {BAH} = \widehat {ACH}\) (gt)
\( \Rightarrow \Delta AHB\backsim\Delta CHA\;(g - g)\)
\( \Rightarrow \) (I) đúng.
Xét $2$ tam giác vuông $AHC$ và $BAC$ có:
\(\widehat C\) chung
\( \Rightarrow \Delta AHC\backsim\Delta BAC\;(g - g)\)
\( \Rightarrow \) (II) đúng.
Vậy cả (I) và (II) đều đúng.
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$.
(II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
Vì $\Delta DHE\backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$ nên tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$ và tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là ${\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}$
Do đó (I) và (IV) đúng, (II) và (III) sai.
Cho tam giác $ABC$ cân tại $A$, đường cao $CE$. Tính $AB$, biết $BC = 24$cm và $BE = 9$cm.
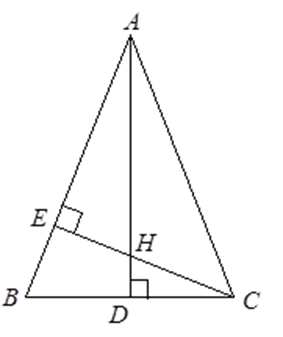
Kẻ đường cao $AD$ . Xét \(\Delta CBE\) và \(\Delta ABD\) có \(\widehat {BEC} = \widehat {ADB} = 90^\circ \) và \(\widehat B\) chung nên
$\Delta CBE\backsim\Delta ABD$ (g.g) $ \Rightarrow \dfrac{{BC}}{{AB}} = \dfrac{{BE}}{{BD}}$ hay $\dfrac{{24}}{{AB}} = \dfrac{9}{{12}}$
$ \Rightarrow AB = 32{\rm{cm}}$.
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
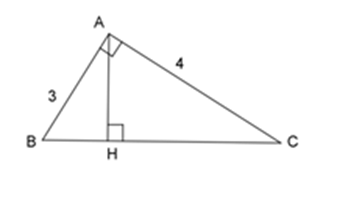
Áp dụng định lý Pytago vào tam giác vuông $ABC$ ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {3^2} + {4^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 25\\ \Rightarrow BC = 5\;cm\end{array}\)
Xét 2 tam giác vuông $ABC$ và $HBA$ có: \(\widehat B\) chung
\( \Rightarrow \Delta ABC\backsim\Delta HBA\;(g - g)\)
\( \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BC}}{{BA}} \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = 1,8\;cm\)
Mặt khác:
\(\dfrac{{AB}}{{HB}} = \dfrac{{AC}}{{HA}} \Rightarrow HA = \dfrac{{AC.HB}}{{AB}} = \dfrac{{4.1,8}}{3} = 2,4\;cm\)
Nên \(HA = 2,4\,cm;\,HB = 1,8\,cm\) .
Cho tam giác $ABC$ cân tại $A$ , $AC = 20{\rm{cm}}$, $BC = 24{\rm{cm}}$, các đường cao $AD$ và $CE$ cắt nhau ở $H$ . Tính độ dài \(HD\) .
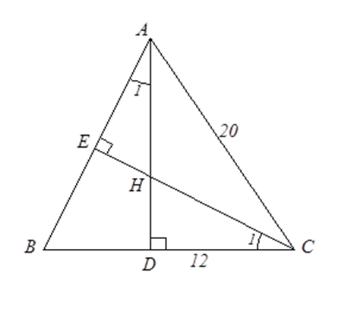
Tam giác $ABC$ cân tại $A$ nên $BD = DC = \dfrac{{BC}}{2} = \dfrac{{24}}{2} = 12\left( {{\rm{cm}}} \right)$.
Theo định lý Py-ta-go, ta có $A{D^2} = A{C^2} - D{C^2} = {20^2} - {12^2} = {16^2}$ nên $AD = 16{\rm{cm}}$.
Xét $\Delta CDH$ và $\Delta ADB$ có
$\widehat {CDH} = \widehat {ADB} = {90^o}$ .
$\widehat {{C_1}} = \widehat {{A_1}}$ (cùng phụ với $\widehat B$).
Do đó \(\Delta CDH\backsim\Delta ADB\) (g.g)
Nên $\dfrac{{HD}}{{BD}} = \dfrac{{HC}}{{AB}} = \dfrac{{CD}}{{AD}}$, tức là $\dfrac{{HD}}{{12}} = \dfrac{{HC}}{{20}} = \dfrac{{12}}{{16}} = \dfrac{3}{4}$
Suy ra $HD = 9{\rm{cm}}$.
Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?
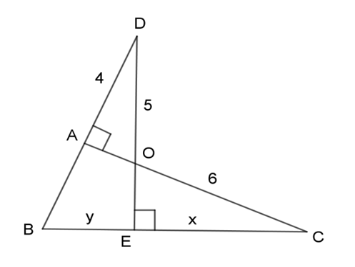
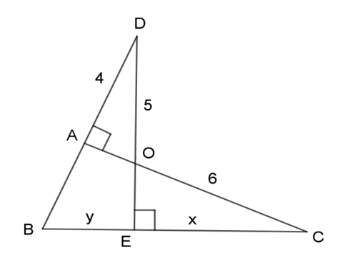
Xét 2 tam giác vuông \(\Delta ADO\)\((\widehat {DAO} = {90^0})\) và \(\Delta ECO\)\((\widehat {CEO} = {90^0})\) ta có:
\(\widehat {AOD} = \widehat {EOC}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta ADO\backsim\Delta ECO\;(g - g)\)
\( \Rightarrow \dfrac{{AD}}{{EC}} = \dfrac{{DO}}{{CO}} \Leftrightarrow \dfrac{4}{x} = \dfrac{5}{6} \Leftrightarrow x = \dfrac{{4.6}}{5} = 4,8\)
Vì \(\Delta ADO\) vuông tại A nên áp dụng định lý Pitago ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,A{D^2} + A{O^2} = O{D^2}\\ \Leftrightarrow {4^2} + A{O^2} = {5^2}\\ \Leftrightarrow A{O^2} = {5^2} - {4^2} = 9\\ \Rightarrow AO = 3\end{array}\)
Xét 2 tam giác vuông \(\Delta CEO\;(\widehat {CEO} = {90^0})\) và \(\Delta CAB\;(\widehat {CAB} = {90^0})\) có:\(\widehat C\) chung
\( \Rightarrow \dfrac{{CO}}{{CB}} = \dfrac{{CE}}{{CA}} \Leftrightarrow \dfrac{{CO}}{{CE + EB}} = \dfrac{{CE}}{{CO + OA}} \Leftrightarrow \dfrac{6}{{4,8 + y}} = \dfrac{{4,8}}{{6 + 3}} \Leftrightarrow y = 6,45\)
Vậy \(x = 4,8;\;y = 6,45\).
Cho tam giác $ABC$ vuông ở $A$ , đường cao $AH$ .
Tích \(HB.HC\) bằng

Ta có: \(\widehat {HAB} + \widehat {HAC} = \widehat {BAC} = {90^0}\)
Mà: \(\widehat {HBA} + \widehat {HAB} = {90^0}\) (2 góc phụ nhau)
\( \Rightarrow \widehat {HAC} = \widehat {HBA}\)
Xét 2 tam giác vuông AHB và CHA ta có: \(\widehat {HAC} = \widehat {HBA}\) (cmt)
\( \Rightarrow \Delta AHB\backsim\Delta CHA\;(g - g)\)
\( \Rightarrow \dfrac{{AH}}{{CH}} = \dfrac{{HB}}{{HA}} \Leftrightarrow A{H^2} = HB.HC\)
Cho tam giác $ABC$ vuông ở $A$ , đường cao $AH$ .
Cho $BH = 9cm,HC = 16cm$ . Tính diện tích của tam giác \(ABC\) .
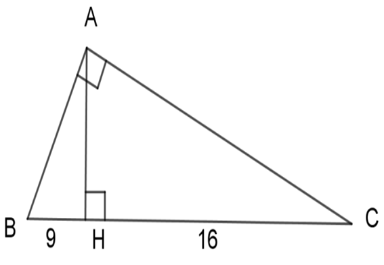
Với $BH = 9cm,HC = 16cm$ .
\( \Rightarrow BC = BH + HC \)\(= 9 + 16 = 25\;cm\)
Ta có: \(A{H^2} = HB.HC\) (cmt)
\(\begin{array}{l} \Rightarrow A{H^2} = 9.16 = 144\\ \Rightarrow AH = 12\;cm\end{array}\)
Nên diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.12.25 = 150\,c{m^2}\) .
Cho tam giác $ABC$ vuông ở $A,AB = 6cm,AC = 8cm$ , đường cao $AH$ , đường phân giác $BD$ .
Tính độ dài các đoạn $AD,DC$ lần lượt là

+ Áp dụng định lý Pitago trong tam giác vuông $ABC$ ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {6^2} + {8^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 100\\ \Rightarrow BC = 10\;cm\end{array}\)
+ Vì $BD$ là đường phân giác của tam giác $ABC$ nên áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}}\\ \Leftrightarrow \dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CA - AD}}\)\( \Leftrightarrow \dfrac{6}{{AD}} = \dfrac{{10}}{{8 - AD}}\\ \Rightarrow AD = 3\;cm\\ \Rightarrow DC = AC - AD \)\(= 8 - 3 = 5\;cm\)
Cho tam giác $ABC$ vuông ở $A,AB = 6cm,AC = 8cm$ , đường cao $AH$ , đường phân giác $BD$ .
Gọi $I$ là giao điểm của $AH$ và $BD$ . Chọn câu đúng.
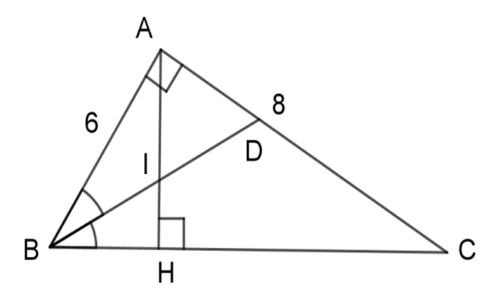
Xét 2 tam giác vuông $ABD$ và $HBI$ có:
\(\widehat {ABD} = \widehat {HBI}\) ($BD$ là tia phân giác của góc $B$ )
\( \Rightarrow \Delta ABD\backsim\Delta HBI\;(g - g)\)
\( \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BD}}{{BI}}\)\( \Leftrightarrow AB.BI = BD.HB\;\)
Cho tam giác $ABC$, phân giác $AD$ . Gọi $E,F$ lần lượt là hình chiếu của $B$ và $C$ lên $AD$ .
Chọn khẳng định đúng.
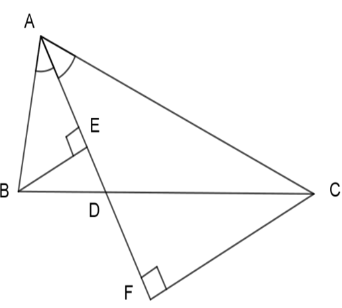
Xét 2 tam giác vuông ABE và ACF ta có:
\(\widehat {BAE} = \widehat {CAF}\) (vì AD là tia phân giác của góc A)
\( \Rightarrow \Delta ABE\backsim\Delta ACF\;(g - g)\)
\( \Rightarrow \dfrac{{AE}}{{AF}} = \dfrac{{BE}}{{CF}}\;(1)\)
Xét 2 tam giác vuông BDE và CDF ta có:
\(\widehat {EDB} = \widehat {FDC}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta BDE\backsim\Delta CDF\)(g – g)
\( \Rightarrow \dfrac{{BE}}{{CF}} = \dfrac{{DE}}{{DF}}\;(2)\)
Từ (1) và (2) ta có:
\(\dfrac{{AE}}{{AF}} = \dfrac{{DE}}{{DF}} \Leftrightarrow AE.DF = AF.DE\) (đpcm)
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ chia cạnh $BC$ thành hai đoạn thẳng $HB = 7$cm và $HC = 18$cm. Điểm $E$ thuộc đoạn thẳng $HC$ sao cho đường thẳng đi qua $E$ và vuông góc với $BC$ chia tam giác $ABC$ thành hai phần có diện tích bằng nhau. Tính $CE$.
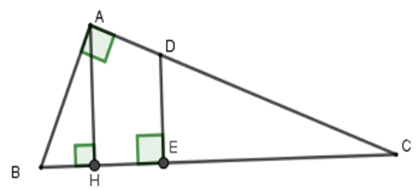
Gọi $D$ là giao điểm của $AC$ và đường vuông góc với $BC$ tại $E$.
Xét \(\Delta AHC\) và \(\Delta ABC\) có \(\widehat C\) chung và \(\widehat {AHC} = \widehat {BAC} = 90^\circ \) nên \(\Delta AHC\backsim\Delta BAC\,\left( {g - g} \right)\)
Ta có ${S_{DEC}} = \dfrac{1}{2}{S_{ABC}}$ (1), ${S_{AHC}}:{S_{ABC}} = \dfrac{{HC}}{{BC}} = \dfrac{{18}}{{25}}$ (2).
Từ (1) và (2) suy ra ${S_{DEC}}:{S_{AHC}} = \dfrac{1}{2}:\dfrac{{18}}{{25}} = \dfrac{{25}}{{36}} = {\left( {\dfrac{5}{6}} \right)^2}$ (3).
Vì \(DE{\rm{//}}AH\) (cùng vuông với \(BC\) ) suy ra $\Delta DEC\backsim\Delta AHC$ nên ${S_{DEC}}:{S_{AHC}} = {\left( {\dfrac{{EC}}{{HC}}} \right)^2}$ (4).
Từ (3) và (4) suy ra $\dfrac{{EC}}{{HC}} = \dfrac{5}{6}$ tức là $\dfrac{{EC}}{{18}} = \dfrac{5}{6} \Rightarrow EC = 15\,{\rm{cm}}$.

