Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ chia cạnh $BC$ thành hai đoạn thẳng $HB = 7$cm và $HC = 18$cm. Điểm $E$ thuộc đoạn thẳng $HC$ sao cho đường thẳng đi qua $E$ và vuông góc với $BC$ chia tam giác $ABC$ thành hai phần có diện tích bằng nhau. Tính $CE$.

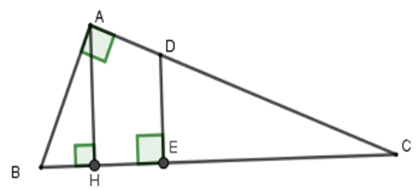
Gọi $D$ là giao điểm của $AC$ và đường vuông góc với $BC$ tại $E$.

Xét \(\Delta AHC\)  và \(\Delta ABC\) có \(\widehat C\) chung và \(\widehat {AHC} = \widehat {BAC} = 90^\circ \)  nên \(\Delta AHC\backsim\Delta BAC\,\left( {g - g} \right)\)

Ta có ${S_{DEC}} = \dfrac{1}{2}{S_{ABC}}$ (1), ${S_{AHC}}:{S_{ABC}} = \dfrac{{HC}}{{BC}} = \dfrac{{18}}{{25}}$ (2).

Từ (1) và (2) suy ra ${S_{DEC}}:{S_{AHC}} = \dfrac{1}{2}:\dfrac{{18}}{{25}} = \dfrac{{25}}{{36}} = {\left( {\dfrac{5}{6}} \right)^2}$  (3).

Vì \(DE{\rm{//}}AH\) (cùng vuông với \(BC\) ) suy ra $\Delta DEC\backsim\Delta AHC$ nên ${S_{DEC}}:{S_{AHC}} = {\left( {\dfrac{{EC}}{{HC}}} \right)^2}$ (4).

Từ (3) và (4) suy ra $\dfrac{{EC}}{{HC}} = \dfrac{5}{6}$ tức là $\dfrac{{EC}}{{18}} = \dfrac{5}{6} \Rightarrow EC = 15\,{\rm{cm}}$.