Cho tam giác $ABC$  cân tại $A$ , $AC = 20{\rm{cm}}$, $BC = 24{\rm{cm}}$, các đường cao $AD$  và $CE$  cắt nhau ở $H$ . Tính độ dài \(HD\) .

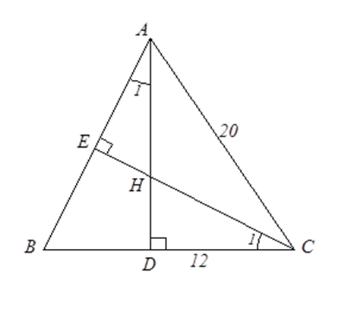
Tam giác $ABC$  cân tại $A$  nên $BD = DC = \dfrac{{BC}}{2} = \dfrac{{24}}{2} = 12\left( {{\rm{cm}}} \right)$.

Theo định lý Py-ta-go, ta có $A{D^2} = A{C^2} - D{C^2} = {20^2} - {12^2} = {16^2}$ nên $AD = 16{\rm{cm}}$.

Xét $\Delta CDH$ và $\Delta ADB$ có

$\widehat {CDH} = \widehat {ADB} = {90^o}$ .

$\widehat {{C_1}} = \widehat {{A_1}}$ (cùng phụ với $\widehat B$).

Do đó  \(\Delta CDH\backsim\Delta ADB\) (g.g)

Nên $\dfrac{{HD}}{{BD}} = \dfrac{{HC}}{{AB}} = \dfrac{{CD}}{{AD}}$, tức là $\dfrac{{HD}}{{12}} = \dfrac{{HC}}{{20}} = \dfrac{{12}}{{16}} = \dfrac{3}{4}$

Suy ra $HD = 9{\rm{cm}}$.