Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(HB = 3,5\)cm và \(HC = 9\)cm. Điểm \(E\) thuộc đoạn thẳng \(HC\) sao cho đường thẳng đi qua \(E\) và vuông góc với \(BC\) chia tam giác \(ABC\) thành hai phần có diện tích bằng nhau. Tính \(CE\).

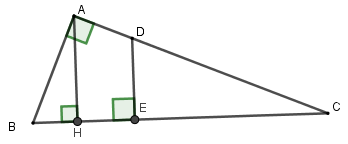
Gọi \(D\) là giao điểm của \(AC\) và đường vuông góc với \(BC\) tại \(E\).

Xét \(\Delta AHC\) và \(\Delta BAC\) có:

\(\widehat C\) chung và \(\widehat {AHC} = \widehat {BAC} = 90^\circ \) nên \(\Delta AHC\backsim\Delta BAC\,\left( {g - g} \right)\)

Ta có: \({S_{DEC}} = \dfrac{1}{2}{S_{ABC}}\) (1), \({S_{AHC}}:{S_{BAC}} = \dfrac{{HC}}{{BC}} = \dfrac{9}{{9 + 3,5}} = \dfrac{{18}}{{25}}\) (2).

Từ (1) và (2) suy ra \({S_{DEC}}:{S_{AHC}} = \dfrac{1}{2}:\dfrac{{18}}{{25}} = \dfrac{{25}}{{36}} = {\left( {\dfrac{5}{6}} \right)^2}\)  (3).

Vì \(DE{\rm{//}}AH\) (cùng vuông với \(BC\)) suy ra \(\Delta DEC\backsim\Delta AHC\) nên \({S_{DEC}}:{S_{AHC}} = {\left( {\dfrac{{EC}}{{HC}}} \right)^2}\) (4).

Từ (3) và (4) suy ra \(\dfrac{{EC}}{{HC}} = \dfrac{5}{6}\) tức là \(\dfrac{{EC}}{9} = \dfrac{5}{6} \Rightarrow EC = 7,5\,{\rm{cm}}\).