Cho \(\Delta ABC\), \(AE\) là phân giác ngoài của góc A. Hãy chọn câu đúng:
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hoai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên \(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\)
Cho \(\Delta MNP,MA\) là phân giác ngoài của góc $M$ , biết \(\dfrac{{NA}}{{PA}} = \dfrac{3}{4}\). Hãy chọn câu đúng.
Theo tính chất đường phân giác của tam giác ta có \(\dfrac{{MN}}{{MP}} = \dfrac{{NA}}{{PA}} = \dfrac{3}{4}\)
Cho tam giác $ABC$ , $AC = 2AB$ , $AD$ là đường phân giác của tam giác $ABC$ , khi đó \(\dfrac{{BD}}{{CD}} = ?\)
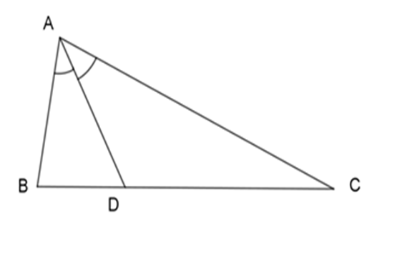
Vì $AD$ là phân giác của \(\Delta ABC\) nên: \(\dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{DC}}\)
Theo bài, ta có: $AC = 2AB$
\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{1}{2} \Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{1}{2}\)
Cho tam giác $ABC$ cân tại $A$ , đường phân giác trong của góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 15$ $cm$ , $BC = 10cm$ . Khi đó $AD = $ ?
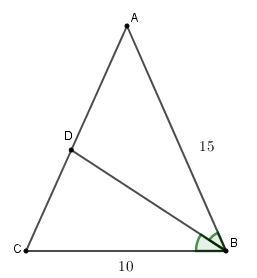
Vì $BD$ là đường phân giác của \(\widehat {ABC}\) nên:
\(\dfrac{{AD}}{{DC}} = \dfrac{{AB}}{{BC}}\)
Suy ra: \(\dfrac{{AD}}{{DC + AD}} = \dfrac{{AB}}{{BC + AB}}\)
(theo tính chất dãy tỉ số bằng nhau)
\( \Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{{AB}}{{BC + AB}}\)
Mà tam giác $ABC$ cân tại $A$ nên $AC = AB = 15cm.$\( \Rightarrow \dfrac{{AD}}{{15}} = \dfrac{{15}}{{15 + 10}} \)\(\Rightarrow AD = \dfrac{{15.15}}{{25}} = 9\;cm\)
Cho tam giác $ABC$ , \(\widehat A = {90^0}\), $AB = 15 cm, AC = 20 cm,$ đường cao $AH$ \((H \in BC)\). Tia phân giác của \(\widehat {HAB}\) cắt $HB$ tại $D$ . Tia phân giác của \(\widehat {HAC}\) cắt $HC$ tại $E$ . Tính $DH$ ?
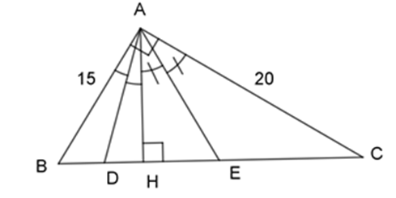
Áp dụng định lý Pytago vào tam giác $ABC$ vuông tại$A$ , ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {15^2} + {20^2} = B{C^2}\\ \Rightarrow BC = 25\end{array}\)
Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}.AH.BC\)
\( \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{15.20}}{{25}} = 12\)
Áp dụng định lý Pitago trong tam giác $AHB$ vuông tại$H$ , ta có:
\(\begin{array}{l}\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2}\\ \Leftrightarrow {15^2} = {12^2} + H{B^2}\\ \Rightarrow H{B^2} = 81 \Rightarrow HB = 9\\ \Rightarrow HC = BC - HB = 25 - 9 = 16.\end{array}\)
Vì $AD$ là phân giác của tam giác $ABH$ nên:
\(\begin{array}{l}\dfrac{{AB}}{{AH}} = \dfrac{{BD}}{{DH}} \Leftrightarrow \dfrac{{AB}}{{AH}} = \dfrac{{BH - DH}}{{DH}}\\ \Leftrightarrow \dfrac{{15}}{{12}} = \dfrac{{9 - DH}}{{DH}} \Leftrightarrow 15DH = 108 - 12DH \Leftrightarrow DH = 4\,cm.\end{array}\)
Cho tam giác $ABC,AB = AC = 10cm,$$BC = 12cm.$ Gọi $I$ là giao điểm của các đường phân giác của tam giác $ABC.$ Tính $BI$ ?
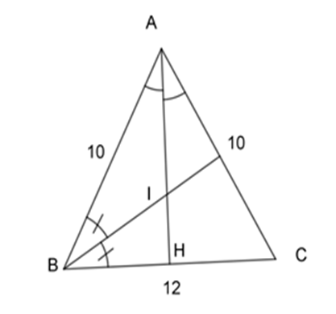
- Ta có $AB = AC = 10 cm$
Suy ra \(\Delta ABC\) cân tại A.
- Có I là giao các đường phân giác của \(\Delta ABC\).
Suy ra $AI, BI$ là đường phân giác của \(\Delta ABC\).
- Gọi $H$ là giao của $AI$ và $BC.$
- Khi đó ta có $AH$ vừa là đường phân giác, vừa là đường cao,
vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân $ABC$ (tính chất tam giác cân).
\( \Rightarrow \) $H$ là trung điểm của cạnh $BC$ \( \Rightarrow BH = HC = \dfrac{{BC}}{2} = \dfrac{{12}}{2} = 6\;cm\).
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,A{H^2} + B{H^2} = A{B^2}\\ \Leftrightarrow A{H^2} + {6^2} = {10^2}\\ \Leftrightarrow A{H^2} = 100 - 36 = 64\\ \Rightarrow AH = 8\end{array}\)
Vì $BI$ là phân giác của tam giác $ABH$ nên:
\(\begin{array}{l}\dfrac{{AB}}{{BH}} = \dfrac{{AI}}{{IH}} = \dfrac{{AH - IH}}{{IH}}\\ \Leftrightarrow \dfrac{{10}}{6} = \dfrac{{8 - IH}}{{IH}}\\ \Leftrightarrow 10IH = 48 - 6IH\\ \Leftrightarrow IH = 3\end{array}\)
Áp dụng định lý Pitago trong tam giác $BHI$ vuông tại $H,$ ta có:
$\begin{array}{l}\,\,\,\,\,\,\,\,B{I^2} = I{H^2} + B{H^2}\\ \Leftrightarrow B{I^2} = {3^2} + {6^2}\\ \Leftrightarrow B{I^2} = 45\\ \Rightarrow BI = 3\sqrt 5 \end{array}$
Cho tam giác $ABC$ có chu vi $18cm$ , các đường phân giác $BD$ và $CE$ . Tính các cạnh của tam giác $ABC$ , biết $\dfrac{{AD}}{{DC}} = \dfrac{1}{2},\dfrac{{AE}}{{EB}} = \dfrac{3}{4}$.
Theo tính chất đường phân giác, ta có
$\dfrac{{AB}}{{BC}} = \dfrac{{AD}}{{DC}} = \dfrac{1}{2},$
$\dfrac{{AC}}{{BC}} = \dfrac{{AE}}{{EB}} = \dfrac{3}{4}$nên
$\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3},$
Do đó $\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3} = \dfrac{{AB + BC + AC}}{{2 + 4 + 3}} = \dfrac{{18}}{9} = 2$.
Vậy $AB = 4\,cm,BC = 8\,cm,AC = 6\,cm.$
Cho tam giác $ABC$ , đường trung tuyến $AM$ . Tia phân giác của góc $AMB$ cắt $AB$ ở $D$ , tia phân giác của góc $AMC$ cắt $AC$ ở$E$ . Gọi $I$ là giao điểm của $AM$ và $DE$ .
Chọn khẳng định đúng.
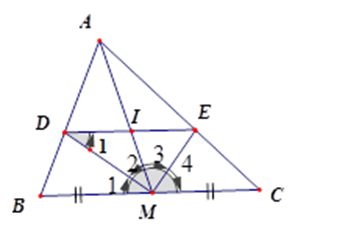
Vì \(MD\) và \(ME\) lần lượt là phân giác của \(\widehat {AMB};\,\widehat {AMC}\) nên \(\dfrac{{DA}}{{DB}} = \dfrac{{MA}}{{MB}},\dfrac{{EA}}{{EC}} = \dfrac{{MA}}{{MC}}\)
mà $MB = MC$ nên \(\dfrac{{DA}}{{DB}} = \dfrac{{EA}}{{EC}} \Rightarrow DE{\rm{//}}BC\)( định lí Ta-lét đảo).
Vì \(DE{\rm{//}}BC\) nên \(\dfrac{{DI}}{{BM}} = \dfrac{{AI}}{{AM}} = \dfrac{{IE}}{{MC}}\) (hệ quả định lý Ta-lét) mà $BM = MC$ nên $DI = IE$ .
Nên cả A, B đều đúng.
Cho tam giác $ABC$ , đường trung tuyến $AM$ . Tia phân giác của góc $AMB$ cắt $AB$ ở $D$ , tia phân giác của góc $AMC$ cắt $AC$ ở$E$ . Gọi $I$ là giao điểm của $AM$ và $DE$ .
Tính độ dài $DE$ , biết $BC = 30cm,AM = 10cm$ .
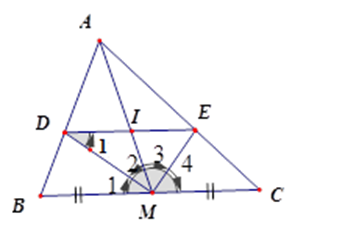
Vì $DI = IE$ (cmt) nên $MI$ là đường trung tuyến của tam giác $MDE$ .
\(\Delta MDE\) vuông ( vì $MD,ME$ là tia phân giác của góc kề bù) nên$MI = DI = IE$ .
Đặt$DI = MI = x$ , ta có $\dfrac{{DI}}{{BM}} = \dfrac{{AI}}{{AM}}$ (cmt) nên $\dfrac{x}{{15}} = \dfrac{{10 - x}}{{10}}.$ Từ đó x= 6 suy ra $DE = 12cm$ .

