Cho tam giác $ABC$ , đường trung tuyến $AM$ . Tia phân giác của góc $AMB$ cắt $AB$ ở $D$ , tia phân giác của góc $AMC$ cắt $AC$ ở$E$ . Gọi $I$ là giao điểm của $AM$ và $DE$ .
Tính độ dài $DE$ , biết $BC = 30cm,AM = 10cm$ .
Trả lời bởi giáo viên
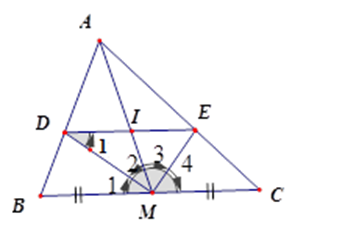
Vì $DI = IE$ (cmt) nên $MI$ là đường trung tuyến của tam giác $MDE$ .
\(\Delta MDE\) vuông ( vì $MD,ME$ là tia phân giác của góc kề bù) nên$MI = DI = IE$ .
Đặt$DI = MI = x$ , ta có $\dfrac{{DI}}{{BM}} = \dfrac{{AI}}{{AM}}$ (cmt) nên $\dfrac{x}{{15}} = \dfrac{{10 - x}}{{10}}.$ Từ đó x= 6 suy ra $DE = 12cm$ .
Hướng dẫn giải:
- Sử dụng tính chất: Hai tia phân giác của hai góc kề bì thì vuông góc với nhau để suy ra các cạnh bằng nhau nhờ tính chất đường trung tuyến trong tam giác vuông.
- Sử dụng định lý Ta-lét để có các tỉ số thích hợp tính \(DE\) .