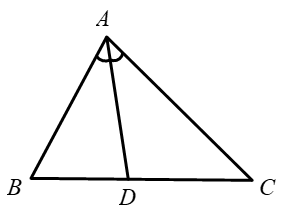
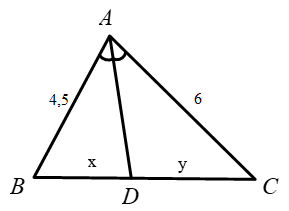
Cho hình vẽ, biết rằng các số trên hình có cùng đơn vị đo. Tính giá trị biểu thức \(S = 49{x^2} + 98{y^2}\).

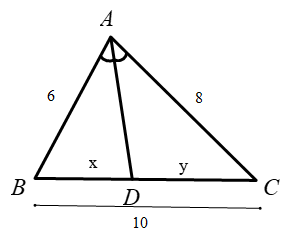
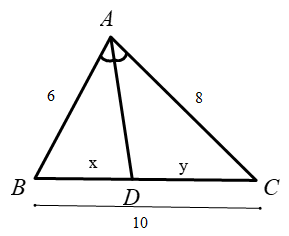
Vì \(AD\) là phân giác \(\widehat {BAC}\) nên ta có:

\(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}} = \dfrac{6}{8} = \dfrac{3}{4}\) \( \Rightarrow \dfrac{{BD}}{3} = \dfrac{{DC}}{4}\).

Theo tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{{BD}}{3} = \dfrac{{DC}}{4} = \dfrac{{BD + DC}}{{3 + 4}} = \dfrac{{10}}{7}\)

\( \Rightarrow BD = 3.\dfrac{{10}}{7} = \dfrac{{30}}{7};\) \(DC = 4.\dfrac{{10}}{7} = \dfrac{{40}}{7}\)

Do đó \(x = \dfrac{{30}}{7},y = \dfrac{{40}}{7}\) \( \Rightarrow S = 49{x^2} + 98{y^2}\) \( = 49.{\left( {\dfrac{{30}}{7}} \right)^2} + 98.{\left( {\dfrac{{40}}{7}} \right)^2} = 4100\)

Vậy \(S = 4100\).