Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có chu vi $18cm$ , các đường phân giác $BD$ và $CE$ . Tính các cạnh của tam giác $ABC$ , biết $\dfrac{{AD}}{{DC}} = \dfrac{1}{2},\dfrac{{AE}}{{EB}} = \dfrac{3}{4}$.
Trả lời bởi giáo viên
Đáp án đúng: c
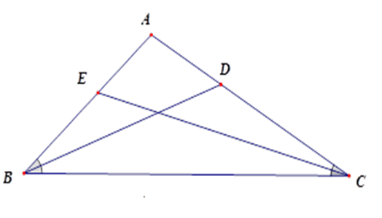
Theo tính chất đường phân giác, ta có
$\dfrac{{AB}}{{BC}} = \dfrac{{AD}}{{DC}} = \dfrac{1}{2},$
$\dfrac{{AC}}{{BC}} = \dfrac{{AE}}{{EB}} = \dfrac{3}{4}$nên
$\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3},$
Do đó $\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3} = \dfrac{{AB + BC + AC}}{{2 + 4 + 3}} = \dfrac{{18}}{9} = 2$.
Vậy $AB = 4\,cm,BC = 8\,cm,AC = 6\,cm.$
Hướng dẫn giải:
Bước 1: Sử dụng tính chất đường phân giác của tam giác.
Bước 2: Sử dụng tính chất tỉ lệ thức để biến đổi.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
