Câu hỏi:
2 năm trước
Cho tam giác $ABC$ , đường trung tuyến $AM$ . Tia phân giác của góc $AMB$ cắt $AB$ ở $D$ , tia phân giác của góc $AMC$ cắt $AC$ ở$E$ . Gọi $I$ là giao điểm của $AM$ và $DE$ .
Chọn khẳng định đúng.
Trả lời bởi giáo viên
Đáp án đúng: d
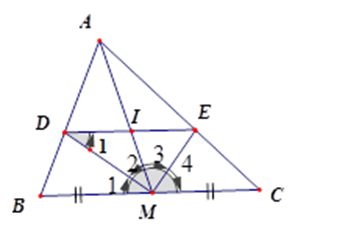
Vì \(MD\) và \(ME\) lần lượt là phân giác của \(\widehat {AMB};\,\widehat {AMC}\) nên \(\dfrac{{DA}}{{DB}} = \dfrac{{MA}}{{MB}},\dfrac{{EA}}{{EC}} = \dfrac{{MA}}{{MC}}\)
mà $MB = MC$ nên \(\dfrac{{DA}}{{DB}} = \dfrac{{EA}}{{EC}} \Rightarrow DE{\rm{//}}BC\)( định lí Ta-lét đảo).
Vì \(DE{\rm{//}}BC\) nên \(\dfrac{{DI}}{{BM}} = \dfrac{{AI}}{{AM}} = \dfrac{{IE}}{{MC}}\) (hệ quả định lý Ta-lét) mà $BM = MC$ nên $DI = IE$ .
Nên cả A, B đều đúng.
Hướng dẫn giải:
+ Sử dụng tính chat đường phân giác của tam giác.
+ Sử dụng định lý Ta-lét và hệ quả của định lý Ta-lét.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
