Các bài toán về đường thẳng và mặt phẳng

Gọi \(I\left( {a;b;c} \right)\) là điểm thỏa mãn đẳng thức : \(2\overrightarrow {IA}  + 3\overrightarrow {IB}  = \overrightarrow 0 \)

\(\begin{array}{l} \Rightarrow 2\left( {2 - a; - 2 - b;4 - c} \right) + 3\left( { - 3 - a;3 - b; - 1 - c} \right) = \overrightarrow 0 \\ \Rightarrow \left\{ \begin{array}{l}4 - 2a - 9 - 3a = 0\\ - 4 - 2b + 9 - 3b = 0\\8 - 2c - 3 - 3c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 5a - 5 = 0\\ - 5b + 5 = 0\\ - 5c + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\\c = 1\end{array} \right. \Rightarrow I\left( { - 1;\;1;\;1} \right)\end{array}\)

Ta có :

\(\begin{array}{l}2M{A^2} + 3M{B^2} = 2{\overrightarrow {MA} ^2} + 3{\overrightarrow {MB} ^2}\\ = 2{\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + 3{\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2}\\ = 5M{I^2} + \left( {2I{A^2} + 3I{B^2}} \right) + \overrightarrow {MI} \left( {2\overrightarrow {IA}  + 3\overrightarrow {IB} } \right)\\ = 5M{I^2} + \left( {2I{A^2} + 3I{B^2}} \right)\end{array}\)

Do I, A, B cố định nên \(2I{A^2} + 3I{B^2} = const\).

 \( \Rightarrow {\left( {2M{A^2} + 3M{B^2}} \right)_{\min }} \Leftrightarrow 5M{I^2}_{\min }\)\( \Leftrightarrow \) M là hình chiếu của I trên (P)

Gọi \(\left( \Delta  \right)\) là đường thẳng đi qua I vuông góc với (P) , ta có phương trình của \(\left( \Delta  \right):\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 1 - t\\z = 1 + 2t\end{array} \right.\).

M là hình chiếu của I lên (P) \( \Rightarrow M \in \left( \Delta  \right) \Rightarrow M\left( { - 1 + 2t;1 - t;1 + 2t} \right)\) .

Lại có \(M \in \left( P \right)\)  

\(\begin{array}{l} \Rightarrow 2\left( { - 1 + 2t} \right) - \left( {1 - t} \right) + 2\left( {1 + 2t} \right) - 8 = 0\\ \Leftrightarrow  - 2 + 4t - 1 + t + 2 + 4t - 8 = 0\\ \Leftrightarrow 9t - 9 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {1;0;3} \right)\end{array}\)

Khi đó ta có

\(\begin{array}{l}M{I^2} = 4 + 1 + 4 = 9;\;\;\;I{A^2} = 9 + 9 + 9 = 27;\;\;\;I{B^2} = 4 + 4 + 4 = 13\\ \Rightarrow {\left( {2M{A^2} + 3M{B^2}} \right)_{\min }} = 5.9 + 2.27 + 3.12 = 135\end{array}\)

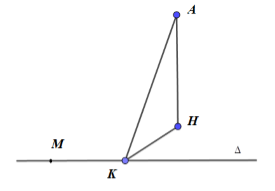
Do \(\Delta \) là đường thẳng đi qua \(M\left( {0;0;2} \right)\) và song song với mặt phẳng \(\left( P \right):x + y + z + 3 = 0\) \( \Rightarrow \Delta  \subset \left( Q \right)\): qua M và song song \(\left( P \right)\).

Phương trình mặt phẳng (Q) là: \(x + y + z - 2 = 0\).

Dựng \(AH \bot \left( Q \right),AK \bot \Delta \). Ta có: \(AK \ge AH\). Do đó, khoảng cách từ \(A\left( {5;0;0} \right)\) đến đường thẳng \(\Delta \) nhỏ nhất và bằng AH khi và chỉ khi K trùng H

Khi đó, đường thẳng \(\Delta \) được xác định là đường thẳng đi qua M và H.

Phương trình đường thẳng AH là \(\left\{ \begin{array}{l}x = 5 + t\\y = t\\z = t\end{array} \right. \Rightarrow \)Giả sử \(H\left( {5 + t;t;t} \right) \Rightarrow 5 + t + t + t - 2 = 0 \Leftrightarrow t =  - 1 \Rightarrow H\left( {4; - 1; - 1} \right)\)

\( \Rightarrow \overrightarrow {MH}  = \left( {4; - 1; - 3} \right) \Rightarrow \Delta \) có 1 VTCP là \(\overrightarrow {{u_3}}  = \left( {4; - 1; - 3} \right)\).

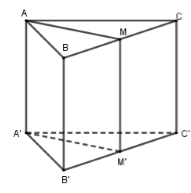
Phương trình \(BC \equiv Oz:\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right.\).

Mặt phẳng \(\left( {AMM'A'} \right)\) đi qua \(A'\) và vuông góc với \(BC\) nên \(\left( {AMM'A'} \right)\) đi qua \(A'\left( {\sqrt 3 ; - 1;1} \right)\) và nhận \(\overrightarrow k  = \left( {0;0;1} \right)\) làm VTPT hay \(\left( {AMM'A'} \right):0\left( {x - \sqrt 3 } \right) + 0\left( {y + 1} \right) + 1\left( {z - 1} \right) = 0 \Leftrightarrow z = 1\).

\(M = BC \cap \left( {AMM'A'} \right) \Rightarrow t - 1 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {0;0;1} \right)\)

Mà \(AA' = 1,A'M = \sqrt {{{\left( {\sqrt 3  - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2} + {{\left( {1 - 1} \right)}^2}}  = 2\) \( \Rightarrow AM = \sqrt {A'{M^2} - A'{A^2}}  = \sqrt {{2^2} - {1^2}}  = \sqrt 3 \).

Tam giác \(ABC\) đều có độ dài đường cao \(AM = \dfrac{{BC\sqrt 3 }}{2} = \sqrt 3  \Rightarrow BC = 2\)

Gọi \(B\left( {0;0;m} \right),C\left( {0;0;n} \right)\) với \(n \ne 0\) thì \(BC = 2 \Leftrightarrow \left| {m - n} \right| = 2\) và \(M\left( {0;0;1} \right)\) là trung điểm \(BC \Leftrightarrow \dfrac{{m + n}}{2} = 1 \Leftrightarrow m + n = 2\).

Khi đó \(m = 0,n = 2\) vì \(n \ne 0\) hay \(C\left( {0;0;2} \right)\).

\( \Rightarrow \overrightarrow {A'C}  = \left( { - \sqrt 3 ;1;1} \right)\) hay \(2\overrightarrow {AC'}  = \left( { - 2\sqrt 3 ;2;2} \right)\) là một VTCP của \(A'C\).

Suy ra \(a =  - 2\sqrt 3 ,b = 2 \Rightarrow {a^2} + {b^2} = {\left( { - 2\sqrt 3 } \right)^2} + {2^2} = 16\).

Gọi \(N = d \cap \Delta \). Giả sử \(N\left( {2 - 2t;\,\,8 + t;\,\,t} \right) \Rightarrow \overrightarrow {MN}  = \left( { - 2t;\,\,7 + t;\,\,t - 1} \right)\).

Đường thẳng \(\Delta :\,\,\dfrac{{x - 2}}{{ - 2}} = \dfrac{{y - 8}}{1} = \dfrac{z}{1}\) có 1 VTCP là \(\overrightarrow {{u_\Delta }}  = \left( { - 2;1;1} \right)\), đường thẳng \(d\) nhận \(\overrightarrow {MN} \) là 1 VTPT.

Do \(d \bot \Delta \) nên \(\overrightarrow {MN} .\overrightarrow {{u_\Delta }}  = 0\).

\(\begin{array}{l} \Leftrightarrow  - 2t.\left( { - 2} \right) + \left( {7 + t} \right).1 + \left( {t - 1} \right).1 = 0\\ \Leftrightarrow 6t + 6 = 0 \Leftrightarrow t =  - 1\\ \Rightarrow \overrightarrow {MN}  = \left( {2;6; - 2} \right)\end{array}\)

\( \Rightarrow \) Đường thẳng \(d\) đi qua \(M\left( {2;1;1} \right)\) và có 1 VTCP \(\overrightarrow {{u_d}}  = \dfrac{1}{2}\overrightarrow {MN}  = \left( {1;3; - 1} \right)\) có phương trình là: \(\left\{ \begin{array}{l}x = 2 + t'\\y = 1 + 3t'\\z = 1 - t'\end{array} \right.\).

Khi đó, giao điểm của \(d\) và mặt phẳng \(\left( {Oyz} \right)\) ứng với \(t'\) thỏa mãn \(x = 2 + t' = 0 \Leftrightarrow t' =  - 2\).

\( \Rightarrow \) Tọa độ giao điểm của \(d\) và mặt phẳng \(\left( {Oyz} \right)\) là: \(\left( {0; - 5;3} \right)\).

Gọi \(M = d \cap {\Delta _1} \Rightarrow M\left( {1 + {t_1};\,\, - 2 + 4{t_1};\,\,2 + 3{t_1}} \right)\), \(N = d \cap {\Delta _2} \Rightarrow N\left( { - 4 + 5{t_2};\,\, - 7 + 9{t_2};\,\,{t_2}} \right)\).

\( \Rightarrow \overrightarrow {MN}  = \left( {5{t_2} - {t_1} - 5;\,\,9{t_2} - 4{t_1} - 5;\,\,{t_2} - 3{t_1} - 2} \right)\).

Vì \(d \bot \left( P \right):\,\,4y - z + 3 = 0\) có 1 VTPT là \(\overrightarrow n \left( {0;4; - 1} \right)\) nên \(\overrightarrow {MN} \) và \(\overrightarrow n \) là 2 vectơ cùng phương.

\( \Rightarrow \overrightarrow {MN}  = k\overrightarrow n \,\,\left( {k \ne 0} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}5{t_2} - {t_1} - 5 = 0\\9{t_2} - 4{t_1} - 5 = 4k\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\)  \( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\9{t_2} - 4{t_1} - 5 = 4k\\4{t_2} - 12{t_1} - 8 =  - 4k\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\13{t_2} - 16{t_1} - 13 = 0\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\13{t_2} - 16\left( {5{t_2} - 5} \right) - 13 = 0\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\ - 67{t_2} + 67 = 0\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{t_2} = 1\\{t_1} = 0\\k = 1\end{array} \right.\) .

\( \Rightarrow M\left( {1;\,\, - 2;\,\,2} \right),\,\,N\left( {1;\,\,2;\,\,1} \right)\) \( \Rightarrow \overrightarrow {MN}  = \left( {0;4; - 1} \right)\).

Vậy phương trình đường thẳng \(d\) đi qua \(M\) và có 1 VTCP \(\overrightarrow {MN} \left( {0;4; - 1} \right)\) là: \(\left\{ \begin{array}{l}x = 1\\y =  - 2 + 4t\\z = 2 - t\end{array} \right.\)

Vì \(M \in d:\,\,\dfrac{x}{{ - 2}} = \dfrac{{y - 1}}{1} = \dfrac{z}{1} \Rightarrow \) Gọi \(M\left( { - 2t;\,\,1 + t;\,\,t} \right)\).

Ta có: \(OM = \sqrt {{{\left( { - 2t} \right)}^2} + {{\left( {1 + t} \right)}^2} + {t^2}}  = \sqrt {6{t^2} + 2t + 1} \).

\(d\left( {M;\left( P \right)} \right) = \dfrac{{\left| {2\left( { - 2t} \right) - \left( {1 + t} \right) + 2t - 2} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} }} = \dfrac{{\left| { - 3t - 3} \right|}}{3} = \left| {t + 1} \right|\).

Theo bài ra ta có: M cách đều gốc tọa độ O và mặt phẳng \(\left( P \right)\)\( \Leftrightarrow \sqrt {6{t^2} + 2t + 1}  = \left| {t + 1} \right|\).

\(\begin{array}{l} \Leftrightarrow 6{t^2} + 2t + 1 = {t^2} + 2t + 1\\ \Leftrightarrow 5{t^2} = 0 \Leftrightarrow t = 0\end{array}\)

\( \Rightarrow M\left( {0;1;0} \right)\)

Vậy có 1 điểm \(M\)  thỏa mãn yêu cầu bài toán là \(M\left( {0;1;0} \right)\).

Ta có \(A\left( {4; - 3;5} \right),B\left( {2; - 5;1} \right)\) nên trung điểm của AB là \(I\left( {3; - 4;3} \right)\).

Đường thẳng \(\left( d \right):\dfrac{{x + 1}}{3} = \dfrac{{y - 5}}{{ - 2}} = \dfrac{{z + 9}}{{13}}\) có 1 VTCP là \(\overrightarrow {{u_d}}  = \left( {3; - 2;13} \right)\).

Mặt phẳng \(\left( P \right)\) vuông góc với d  nên mặt phẳng (P) có 1 VTPT \(\overrightarrow {{n_P}}  = \overrightarrow {{u_d}}  = \left( {3; - 2;13} \right)\).

Mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến là \(\overrightarrow n  = \left( {3; - 2;13} \right)\) và đi qua \(I\left( {3; - 4;3} \right)\) có phương trình là:

\(3\left( {x - 3} \right) - 2\left( {y + 4} \right) + 13\left( {z - 3} \right) = 0\)\( \Leftrightarrow 3x - 2y + 13z - 56 = 0\).

Gọi \(d\) là đường thẳng đi qua \(M\left( { - 1;3;2} \right)\) và vuông góc với mặt phẳng \(\left( P \right):\,\,x - 2y + 4z + 1 = 0\).

\( \Rightarrow \overrightarrow {{u_d}}  = \overrightarrow {{n_P}}  = \left( {1; - 2;4} \right)\).

\( \Rightarrow \) Phương trình đường thẳng là: \(\dfrac{{x + 1}}{1} = \dfrac{{y - 3}}{{ - 2}} = \dfrac{{z - 2}}{4}\).

Bước 1:

Đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = t\\y = t\\z = t\end{array} \right.\) đi qua hai điểm \(O\left( {0;0;0} \right)\) và \(A\left( {1;1;1} \right)\).

Bước 2:

Hình chiếu của điểm \(O,\,\,A\) trên \(\left( {Oxy} \right)\) lần lượt là \(O\left( {0;0;0} \right)\) và \(A'\left( {1;1;0} \right)\).

Bước 3:

Khi đó hình chiếu của \(d\) là đường thẳng \(d'\) đi qua \(O,\,\,A'\), nhận \(\overrightarrow {OA'}  = \left( {1;1;0} \right)\) là 1 VTCP nên có phương trình tham số là \(\left\{ \begin{array}{l}x = t\\y = t\\z = 0\end{array} \right.\).

Bước 1: Viết phương trình mặt phẳng \(\left( P \right)\) là mặt phẳng đi qua \(M\) và vuông góc với \(\Delta \).

Ta có: \(\Delta :\,\,\,\dfrac{x}{1} = \dfrac{{y + 2}}{2} = \dfrac{{z - 1}}{1}\) và \(M\left( {2;\,\,0;\,\,1} \right)\)

Gọi \(\left( P \right)\) là mặt phẳng đi qua \(M\) và vuông góc với \(\Delta \) \( \Rightarrow \overrightarrow {{n_P}}  = \overrightarrow {{u_\Delta }}  = \left( {1;\,\,2;\,\,1} \right).\)

\( \Rightarrow \left( P \right):\,\,\,x - 2 + 2y + z - 1 = 0\) \( \Leftrightarrow x + 2y + z - 3 = 0.\)

Bước 2:  Tìm tọa độ điểm \(H = \left( P \right) \cap \Delta \), khi đó \(H\) là trung điểm của \(MM'\), từ đó tìm tọa độ điểm \(M'\).

Gọi \(H\) là giao điểm của \(\left( P \right)\) và \(\Delta \)

\( \Rightarrow \) Toạ độ của \(H\) là nghiệm của hệ phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\left\{ \begin{array}{l}\dfrac{x}{1} = \dfrac{{y + 2}}{2} = \dfrac{{z - 1}}{1}\\x + 2y + z - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = t\\y =  - 2 + 2t\\z = 1 + t\\x + 2y + z - 3 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = t\\y =  - 2 + 2t\\z = 1 + t\\t - 4 + 4t + 1 + t - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = t\\y =  - 2 + 2t\\z = 1 + t\\t = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 0\\z = 2\end{array} \right. \Rightarrow H\left( {1;\,\,0;\,\,2} \right)\end{array}\)

Ta có: \(M'\) là điểm đối xứng của \(M\) qua \(\Delta \) \( \Rightarrow H\) là trung điểm của \(MM'\) \( \Rightarrow M'\left( {0;\,\,0;\,\,3} \right)\)

Bước 3: Khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến mặt phẳng \(\left( P \right)\)

Ta có: \(\left( {Oxy} \right):\,\,\,z = 0.\)

\( \Rightarrow d\left( {M;\,\,\left( {Oxy} \right)} \right) = \dfrac{{\left| 3 \right|}}{1} = 3.\)

Bước 1: Gọi \(A = d \cap Oxy \Rightarrow \) Tìm tọa độ điểm \(A\).

Mặt phẳng \(Oxy\) có phương trình \(z = 0\).

Gọi \(A = d \cap Oxy \Rightarrow \) Tọa độ của \(A\) là nghiệm của hệ phương trình

\(\left\{ \begin{array}{l}x = 2 - 2t\\y = 0\\z = t\\z = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\\z = 0\end{array} \right.\\\Rightarrow A\left( {2;0;0} \right)\)

Bước 2: Lấy điểm \(B\) bất kì thuộc \(d\). Gọi \(B'\) là điểm đối xứng với \(B\) qua \(Oxy \Rightarrow \) Tìm tọa độ điểm \(B'\).

Lấy \(B\left( {0;0;1} \right) \in d\). Gọi \(B'\) là điểm đối xứng với \(B\) qua \(Oxy \Rightarrow B'\left( {0;0; - 1} \right)\).

Bước 3: \(d'\) là đường thẳng đối xứng với \(d\) qua mặt phẳng \(Oxy\) \( \Rightarrow d'\) đi qua \(A,\,\,B'\). Viết phương trình đường thẳng \(d'\).

\(d'\) là đường thẳng đối xứng với \(d\) qua mặt phẳng \(Oxy\) \( \Rightarrow d'\) đi qua \(A,\,\,B'\).

\( \Rightarrow d'\) nhận \(\overrightarrow {AB'}  = \left( { - 2;0; - 1} \right)//\left( {2;0;1} \right)\) là 1 VTCP \( \Rightarrow d':\,\,\left\{ \begin{array}{l}x = 2 + 2t\\y = 0\\z = t\end{array} \right.\)

=>$a=2, b=2, c=0$

=>$a+b+c=2+2+0=4$

Bước 1: Viết phương trình đường thẳng \(\Delta \) đi qua \(A\) và vuông góc với \(\left( P \right)\).

Gọi \(\Delta \) là đường thẳng đi qua \(A\) và vuông góc với \(\left( P \right)\), phương trình đường thẳng \(\Delta \) là:

\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - 2t\\z =  - 2 - t\end{array} \right.\,\,\,\left( \Delta  \right)\)

Bước 2: Tìm \(H = \Delta  \cap \left( P \right)\).

Vì \(H\) là hình chiếu vuông góc của \(A\) trên \(\left( P \right)\) nên \(H = \Delta  \cap \left( P \right)\) \( \Rightarrow \) Tọa độ điểm \(H\) là nghiệm của hệ phương trình

\(\begin{array}{l}\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - 2t\\z =  - 2 - t\\2x - 2y - z + 7 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - 2t\\z =  - 2 - t\\2 + 4t - 2 + 4t + 2 + t + 7 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - 2t\\z =  - 2 - t\\9t + 9 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t =  - 1\\x =  - 1\\y = 3\\z =  - 1\end{array} \right. \Rightarrow H\left( { - 1;3; - 1} \right)\end{array}\)

Bước 3: Tìm \(a,\,\,b,\,\,c\) và tính tổng.

\( \Rightarrow a =  - 1,\,\,b = 3,\,\,c =  - 1\).

Vậy \(a + b + c =  - 1 + 3 - 1 = 1\).

\(A'\left( {a;b;c} \right)\) là điểm đối xứng với điểm \(A\left( { - 1;0;3} \right)\) qua mặt phẳng \(\left( P \right):x + 3y - 2z - 7 = 0\).

Khi đó, ta có: \(\left\{ \begin{array}{l}\overrightarrow {AA'} //\overrightarrow {{n_{\left( P \right)}}} \\I \in \left( P \right)\end{array} \right.\), với I là trung điểm của AA’

\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{a + 1}}{1} = \dfrac{{b - 0}}{3} = \dfrac{{c - 3}}{{ - 2}}\\\left( {\dfrac{{a - 1}}{2}} \right) + 3.\dfrac{b}{2} - 2.\dfrac{{c + 3}}{2} - 7 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{a + 1}}{1} = \dfrac{b}{3} = \dfrac{{c - 3}}{{ - 2}}\\a + 3b - 2c = 21\end{array} \right.\)

\( \Rightarrow \dfrac{{a + 1}}{1} = \dfrac{b}{3} = \dfrac{{c - 3}}{{ - 2}} = \dfrac{{a + 1 + 3b - 2c + 6}}{{1 + 9 + 4}} = \dfrac{{21 + 1 + 6}}{{14}} = 2\)\( \Rightarrow \left\{ \begin{array}{l}a = 1\\b = 6\\c =  - 1\end{array} \right.\)\( \Rightarrow A'\left( {1;6; - 1} \right)\)

Vậy $a+b+c=1+6+(-1)=6$