Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ
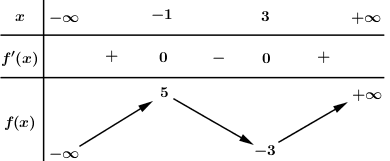
Phương trình |f(3x+1)−2|=5 có bao nhiêu nghiệm?
Đặt t=3x+1.
Dễ thấy với mỗi x chỉ có một x và ngược lại.
Do đó số nghiệm x của phương trình đã cho bằng số nghiệm t của phương trình |f(t)−2|=5
Ta có:
|f(t)−2|=5
⇔[f(t)−2=5f(t)−2=−5⇔[f(t)=7(1)f(t)=−3(2)
Từ bbt ta thấy,
+) Đường thẳng y=7 cắt đồ thị hàm số tại duy nhất 1 điểm nên (1) có 1 nghiệm.
+) Đường thẳng y=−3 cắt đồ thị hàm số tại 2 điểm nên (2) có 2 nghiệm.
Dễ thấy các nghiệm của (1) và (2) phân biệt.
Vậy phương trình đã cho có tất cả 3 nghiệm.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn [−2020;2020] của tham số m để đường thẳng y=x+m cắt đồ thị hàm số y=2x−3x−1 tại hai điểm phân biệt?
TXĐ: D=R∖{1}.
Xét phương trình hoành độ giao điểm:
2x−3x−1=x+m(x≠1)⇔2x−3=(x−1)(x+m)⇔2x−3=x2+mx−x−m⇔x2+(m−3)x−m+3=0(∗)
Để để đường thẳng y=x+m cắt đồ thị hàm số y=2x−3x−1 tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 1
⇒{Δ=(m−3)2−4(−m+3)>01+(m−3).1−m+3≠0⇔{m2−6m+9+4m−12>01≠0(luondung)⇔m2−2m−3>0⇔[m>3m<−1
Kết hợp điều kiện bài toán ta suy ra m∈[−2020;−1)∪(3;2020], m∈Z.
Vậy có 2019 + 2017 = 4036 giá trị của m thỏa mãn yêu cầu bài toán.
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(1−f(x))=2 là:
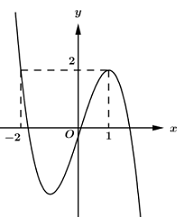
Đặt t=1−f(x), phương trình trở thành f(t)=2.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=2.
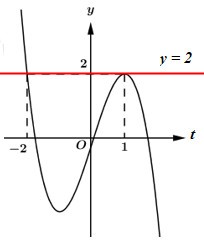
Dựa vào đồ thị hàm số ta thấy f(t)=2⇔[t=1t=−2 ⇔[1−f(x)=11−f(x)=−2⇔[f(x)=0(1)f(x)=3(2).
+ Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số y=f(x) và đường thẳng y=0 nên phương trình (1) có 3 nghiệm phân biệt.
+ Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số y=f(x) và đường thẳng y=3 nên phương trình (1) có 1 nghiệm duy nhất.
Vậy phương trình đã cho có tất cả 4 nghiệm.
Cho hàm số y=f(x) có bảng biến thiên:
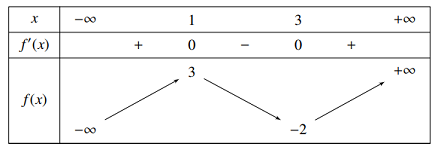
Tìm tất cả các giá trị của m để bất phương trình f(3−x2)≥m vô nghiệm?
Đặt t=3−x2, ta có: x2≥0,∀x∈R⇒t=3−x2≤3,∀x∈R⇒t∈(−∞;3].
Bất phương trình f(3−x2)≥m vô nghiệm khi và chỉ khi f(t)≥m vô nghiệm với mọi t∈(−∞;3].
Từ BBT của hàm số y=f(x) ta thấy: f(t)≥m vô nghiệm với t∈(−∞;3] khi m>3.
Vậy m>3.
Cho hàm số y=x3+2mx2+(m+3)x+4(Cm). Giá trị của tham số m để đường thẳng (d):y=x+4 cắt (Cm) tại ba điểm phân biệt A(0;4),B,C sao cho tam giác KBC có diện tích bằng 8√2 với điểm K(1;3) là:
+ Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng ta có:
x3+2mx2+(m+3)x+4=x+4⇔x3+2mx2+(m+2)x=0⇔x(x2+2mx+m+2)=0⇔[x=0x2+2mx+m+2=0(1)
Để (d) cắt (Cm) tại 3 điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt khác 0
⇒{Δ;>00+2m.0+m+2≠0⇔{m2−m−2>0m≠−2⇔{[m>2m<−1m≠2 .
Gọi x1;x2 là 2 nghiệm phân biệt của phương trình (1) ⇒B(x1;x1+4);C(x2;x2+4).
Khi đó áp dụng định lí Vi-ét ta có: {x1+x2=−2mx1.x2=m+2.
Ta có: SKBC=12.d(K,BC).BC.
Phương trình đường thẳng (d):y=x+4⇔x−y+4=0.
Vì B,C thuộc đường thẳng (d) nên ta có: d(K,BC)=d(K;d)=|1−3+4|√12+(−1)2=√2.
BC=√(x2−x1)2+(x2+4−x1−4)2BC=√2(x1−x2)2BC=√2.√(x1+x2)2−4x1x2BC=√2.√4m2−4(m+2)BC=2√2.√m2−m−2
Theo bài ra ta có:
SKBC=8√2⇔12.√2.2√2√m2−m−2=8√2⇔√m2−m−2=4√2⇔m2−m−2=32⇔m2−m−34=0⇔m=1±√1372(tm)
Vậy m=1±√1372.
Cho hàm số y=x4−4x2+3. Tìm tất cả các giá trị của tham số m sao cho phương trình |x4−4x2+3|=m có 4 nghiệm phân biệt.
Số nghiệm của pt |x4−4x2+3|=m(*) số giao điểm của đồ thị hàm số y=|x4−4x2+3| và đường thẳng y=m.
Ta có đồ thị hàm số y=|x4−4x2+3| như hình vẽ:
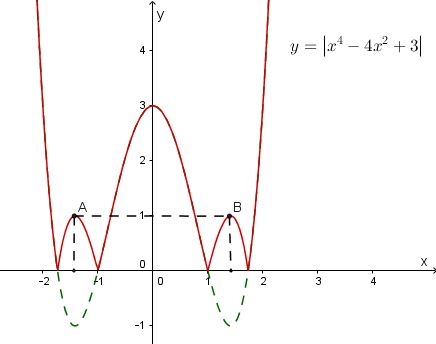
Để pt (∗) có 4 nghiệm phân biệt thì đường thẳng y=m cắt đồ thị hàm số y=|x4−4x2+3| tại 4 điểm phân biệt.
Quan sát đồ thị ta thấy đường thẳng cắt đồ thị hàm số y=|x4−4x2+3| tại 4 điểm phân biệt ⇔[m=01<m<3
Cho y=f(x) là hàm đa thức bậc 3 và có đồ thị như hình vẽ bên. Hỏi phương trình f[f(cosx)−1]=0 có bao nhiêu nghiệm thuộc đoạn [0;3π]?
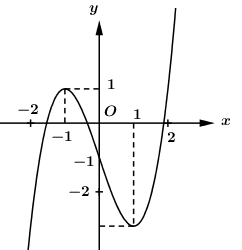
Đặt t=f(cosx)−1, phương trình trở thành: f(t)=0.
Với x∈[0;3π] ⇒−1≤cosx≤1⇔−3≤f(cosx)≤1 ⇒−4≤f(cosx)−1≤0 ⇒t∈[−4;0].
Dựa vào đồ thị hàm số ta thấy f(t)=0⇔[t=t1∈(−2;−1)t=t2∈(−1;0)t=t3∈(1;2)(ktm).
+ Với t=t1⇒f(cosx)−1=t1⇔f(cosx)=t1+1∈(−1;0).
Dựa vào đồ thị hàm số ta có: f(cosx)=t1+1∈(−1;0)⇔[cosx=a1∈(−2;−1)(Vonghiem)cosx=a2∈(−1;0)(1)cosx=a3∈(1;2)(Vonghiem).
Trên đoạn \left[ {0;3\pi } \right] phương trình (1) có 3 nghiệm phân biệt.
+ Với t = {t_2} \Rightarrow f\left( {\cos x} \right) - 1 = {t_2} \Leftrightarrow f\left( {\cos x} \right) = {t_2} + 1 \in \left( {0;1} \right).
Dựa vào đồ thị hàm số ta có: f\left( {\cos x} \right) = {t_2} + 1 \in \left( {0;1} \right) \Leftrightarrow \left[ \begin{array}{l}\cos x = {b_1} \in \left( { - 2; - 1} \right)\,\,\left( {Vo\,\,nghiem} \right)\\\cos x = {b_2} \in \left( {0;1} \right)\,\,\left( 2 \right)\\\cos x = {b_3} \in \left( {1;2} \right)\,\,\left( {Vo\,\,nghiem} \right)\end{array} \right..
Trên đoạn \left[ {0;3\pi } \right] phương trình (2) có 3 nghiệm phân biệt.
Vậy phương trình đã cho có tất cả 6 nghiệm phân biệt.
Cho hàm số y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018 có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ {x_1};{x_2};{x_3}. Tính giá trị biểu thức P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.
Ta có f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018
\Rightarrow f'\left( x \right) = {3.2^{2019}}{x^2} + {3.2^{2019}}x = {3.2^{2019}}x\left( {x + 1} \right) \Rightarrow \dfrac{1}{{f'\left( x \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{1}{{x.\left( {x + 1} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right)
Xét phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018 = 0 (*)
Vì {x_1},{x_2},{x_3} là ba ngiệm của phương trình (*) nên theo hẹ thức Vi-et ta có
\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - 3}}{2}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = 0\\{x_1}{x_2}{x_3} = \dfrac{{2018}}{{{2^{2019}}}}\end{array} \right.
Ta có P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{{{x_1}}} - \dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3}}} - \dfrac{1}{{{x_3} + 1}}} \right)
= \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\left( {\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} + \dfrac{1}{{{x_3}}}} \right) - \left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3} + 1}}} \right)} \right]
= \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3}}}{{{x_1}{x_2}{x_3}}} - \dfrac{{\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right]
= \dfrac{1}{{{{3.2}^{2019}}}}\left( {0 - \dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} + 2\left( {{x_1} + {x_2} + {x_3}} \right) + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right)
= \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{{0 + 2.\dfrac{{ - 3}}{2} + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}} = 0
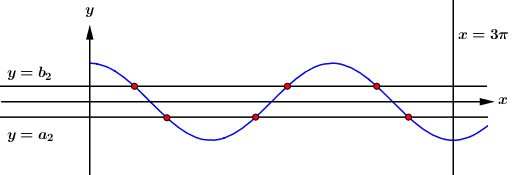
Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} và có đồ thị như hình vẽ. Tổng tất cả giá trị nguyên của tham số m để phương trình f\left( {\sqrt {2f\left( {\cos x} \right)} } \right) = m có nghiệm x \in \left[ {\dfrac{\pi }{2};\pi } \right) là:
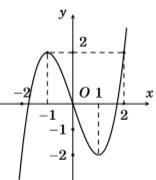
Ta có: - 1 < \cos x \le 0\,\,\,\forall x \in \left[ {\dfrac{\pi }{2};\pi } \right), khi đó dựa vào đồ thị hàm số ta có 0 \le f\left( {\cos x} \right) < 2.
\Leftrightarrow 0 \le 2f\left( {\cos x} \right) < 4 \Leftrightarrow 0 \le \sqrt {2f\left( {\cos x} \right)} < 2.
Đặt t = \sqrt {2f\left( {\cos x} \right)} \Rightarrow t \in \left[ {0;2} \right).
Khi đó yêu cầu bài toán trở thành: Tổng tất cả giá trị nguyên của tham số m để phương trình f\left( t \right) = m có nghiệm t \in \left[ {0;2} \right).
Dựa vào đồ thị hàm số ta thấy với t \in \left[ {0;2} \right) thì f\left( t \right) \in \left[ { - 2;2} \right), do đó phương trình f\left( t \right) = m có nghiệm \Leftrightarrow m \in \left[ { - 2;2} \right).
Mà m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1} \right\}.
Vậy tổng các giá trị của m thỏa mãn là - 2 - 1 + 0 + 1 = - 2.
Cho hàm số y = f\left( x \right) là hàm số đa thức bậc bốn. Biết f\left( 0 \right) = 0 và đồ thị hàm số y = f'\left( x \right) có hình vẽ bên dưới.
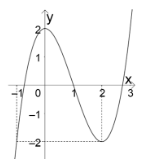
Tập nghiệm của phương trình f\left( {\left| {2\sin x - 1} \right| - 1} \right) = m (với m là tham số) trên đoạn \left[ {0;3\pi } \right] có tối đa bao nhiêu phần tử?
Đặt 2\sin x - 1 = t, với x \in \left[ {0;3\pi } \right] \Rightarrow t \in \left[ { - 3;1} \right].
Vì f'\left( x \right) là hàm đa thức bậc ba nên có dạng f'\left( x \right) = a{x^3} + b{x^2} + cx + d.
Dựa vào đồ thị hàm số ta có: \left\{ \begin{array}{l}a + b + c + d = 0\\c = 0\\ - a + b - c + d = - 2\\d = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 3\\c = 0\\d = 2\end{array} \right. \Rightarrow f'\left( x \right) = {x^3} - 3{x^2} + 2.
Ta có: f\left( 0 \right) = 0 \Rightarrow f\left( x \right) = \dfrac{{{x^4}}}{4} - {x^3} + 2x.
Ta có f'\left( x \right) = {x^3} - 3{x^2} + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1 - \sqrt 3 \\x = 1 + \sqrt 3 \end{array} \right..
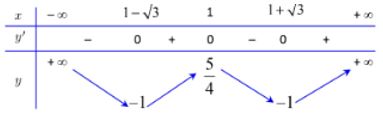
Từ đó suy ra BBT của hàm số y = f\left( {x - 1} \right) như sau:
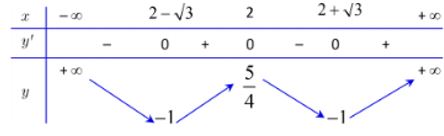
Từ BBT trên ta suy ra BBT của hàm số y = f\left( {\left| x \right| - 1} \right) như sau:
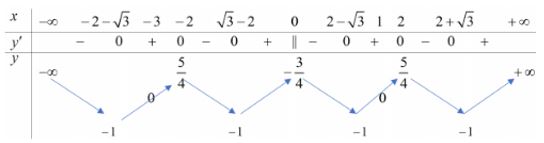
Dựa vào BBT ta thấy phương trình f\left( {\left| t \right| - 1} \right) = m có tối đa 4 nghiệm t \in \left( { - 3;1} \right)
Với mỗi giá trị t \in \left( { - 3;1} \right) thì phương trình 2\sin x - 1 = t có tối đa 4 nghiệm trên \left[ {0;3\pi } \right].
Vậy tập nghiệm của phương trình f\left( {\left| {2\sin x - 1} \right| - 1} \right) = m có tối đa 16 phần tử.
Cho hàm số y = f(x) = a{x^3} + b{x^2} + cx + d có đồ thị như hình dưới đây
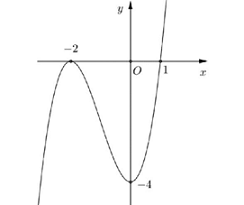
Có tất cả bao nhiêu giá trị nguyên của tham số m \in \left( { - 5;5} \right) để phương trình {f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0 có 6 nghiệm phân biệt
Ta có {f^2}\left( x \right) - \left( {m + 4} \right)\left| {f\left( x \right)} \right| + 2m + 4 = 0
\Leftrightarrow {\left| {f\left( x \right)} \right|^2} - \left( {m + 4} \right)\left| {f\left( x \right)} \right| + 2m + 4 = 0
\Leftrightarrow \left[ \begin{array}{l} \left| {f\left( x \right)} \right| = 2\\ \left| {f\left( x \right)} \right| = m + 2 \end{array} \right.
Dựng đồ thị hàm số y = \left| {f\left( x \right)} \right| ta được:
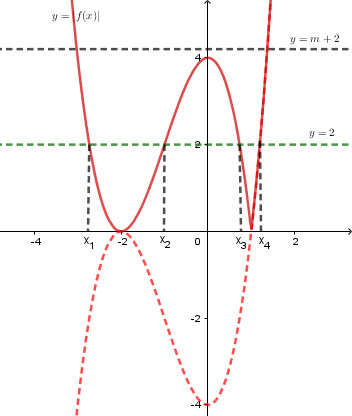
Dễ thấy phương trình \left| {f\left( x \right)} \right| = 2 có 4 nghiệm phân biệt {x_1},{x_2},{x_3},{x_4} nên để phương trình đã cho có 6 nghiệm phân biệt thì phương trình \left| {f\left( x \right)} \right| = m + 2 phải có 2 nghiệm phân biệt khác các nghiệm trên.
Do đó đường thẳng y = m + 2 cắt đồ thị hàm số y = \left| {f\left( x \right)} \right| tại 2 điểm phân biệt.
Từ hình vẽ ta có \left[ \begin{array}{l}m + 2 > 4\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 2\\m = - 2\end{array} \right..
Mà m \in \mathbb{Z} và m \in \left( { - 5;5} \right) nên m \in \left\{ { - 2;3;4} \right\}.
Vậy có 3 giá trị thỏa mãn.
Có bao nhiêu giá trị nguyên của m để phương trình sau có 8 nghiệm thực phân biệt
{\left( {{x^2} - 6\left| x \right| - 1} \right)^2} - \left( {m - 5} \right)\left| x \right|\left( {\left| x \right| - 6} \right) + 1 - m = 0
Ta có:
\begin{array}{l}\,\,\,\,\,\,{\left( {{x^2} - 6\left| x \right| - 1} \right)^2} - \left( {m - 5} \right)\left| x \right|\left( {\left| x \right| - 6} \right) + 1 - m = 0\\ \Leftrightarrow {\left( {{x^2} - 6\left| x \right| - 1} \right)^2} - \left( {m - 5} \right)\left( {{x^2} - 6\left| x \right|} \right) + 1 - m = 0\end{array}
Đặt t = {x^2} - 6\left| x \right|. Khi đó phương trình trở thành:
\begin{array}{l}{\left( {t - 1} \right)^2} - \left( {m - 5} \right)t + 1 - m = 0\\ \Leftrightarrow {t^2} - 2t + 1 - \left( {m - 5} \right)t + 1 - m = 0\\ \Leftrightarrow {t^2} - \left( {m - 3} \right)t + 2 - m = 0\,\,\left( * \right)\end{array}
Xét hàm số f\left( x \right) = {x^2} - 6\left| x \right|, ta vẽ được đồ thị hàm số như sau:
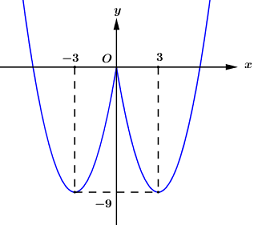
Dựa vào đồ thị hàm số ta thấy phương trình t = {x^2} - 6\left| x \right| có tối đa 4 nghiệm phân biệt, do đó để phương trình ban đầu có 8 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt thỏa mãn - 9 < t < 0.
Xét phương trình (*) ta có:
\begin{array}{l}\Delta = {\left( {m - 3} \right)^2} - 4\left( {2 - m} \right)\\\Delta = {m^2} - 6m + 9 - 8 + 4m\\\Delta = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2}\end{array}
Để phương trình có 2 nghiệm phân biệt thì \Delta > 0 \Leftrightarrow m \ne 1.
Khi đó phương trình có 2 nghiệm phân biệt là \left[ \begin{array}{l}{t_1} = \dfrac{{m - 3 + m - 1}}{2} = m - 2\\{t_2} = \dfrac{{m - 3 - m + 1}}{2} = - 1 \in \left( { - 9;0} \right)\end{array} \right..
Để phương trình có 8 nghiệm phân biệt thì {t_1} \in \left( { - 9;0} \right).
\Rightarrow - 9 < m - 2 < 0 \Leftrightarrow - 7 < m < 2.
Mà m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 6; - 5; - 4; - 3; - 2; - 1;0;1} \right\}.
Kết hợp điều kiện m \ne 1 \Rightarrow m \in \left\{ { - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}
Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán.
Cho hàm số f\left( x \right) có bảng biến thiên như sau:
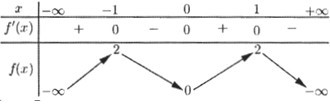
Số nghiệm thuộc đoạn \left[ {0;\dfrac{{5\pi }}{2}} \right] của phương trình f\left( {\sin \,x} \right) = 1 là:
Xét x \in \left[ {0;\dfrac{{5\pi }}{2}} \right]:
Đặt t = \sin x\,\,\left( {t \in \left[ { - 1;1} \right]} \right).
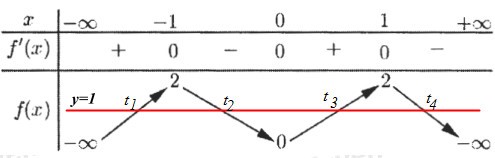
Dựa vào BBT ta thấy phương trình f\left( t \right) = 1 có nghiệm \left[ \begin{array}{l}t = {t_1} < - 1\,\,\,\,\left( {ktm} \right)\\t = {t_2} \in \left( { - 1;0} \right)\\t = {t_3} \in \left( {0;1} \right)\\t = {t_4} > 1\,\,\,\left( {ktm} \right)\end{array} \right.
Suy ra \left[ \begin{array}{l}\sin x = {t_2} \in \left( { - 1;0} \right)\\\sin x = {t_3} \in \left( {0;1} \right)\end{array} \right.
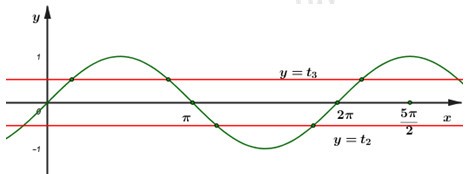
Dựa vào đồ thị hàm số ta thấy,
+) Phương trình \sin x = {t_3} \in \left( {0;1} \right) có 3 nghiệm trong đoạn \left[ {0;\dfrac{{5\pi }}{2}} \right]
+) Phương trình \sin x = {t_2} \in \left( { - 1;0} \right) có 2 nghiệm trong đoạn \left[ {0;\dfrac{{5\pi }}{2}} \right]
Vậy phương trình đã cho có tất cả 5 nghiệm trong đoạn \left[ {0;\dfrac{{5\pi }}{2}} \right].
Tìm m \ne 0 để phương trình {x^2}\left| {x - 3} \right| = m + \dfrac{1}{m} có 4 nghiệm phân biệt.
Số nghiệm của phương trình {x^2}\left| {x - 3} \right| = m + \dfrac{1}{m} là số giao điểm của đường thẳng y = m + \dfrac{1}{m} và đồ thị hàm số y = {x^2}\left| {x - 3} \right|.
Ta có: {x^2}\left| {x - 3} \right| = \left| {{x^2}} \right|.\left| {x - 3} \right| = \left| {{x^2}\left( {x - 3} \right)} \right| = \left| {{x^3} - 3{x^2}} \right|.
Do đó, ta có đồ thị hàm số y = {x^2}\left| {x - 3} \right|:
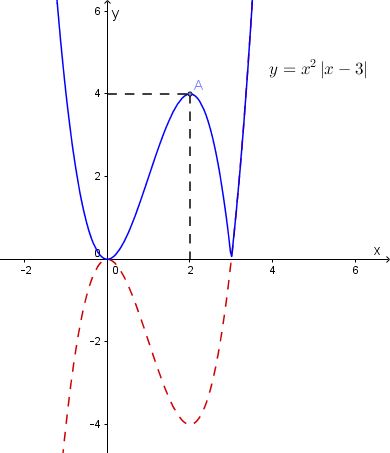
Phương trình {x^2}\left| {x - 3} \right| = m + \dfrac{1}{m} có 4 nghiệm phân biệt \Leftrightarrow đường thẳng y = m + \dfrac{1}{m} cắt đồ thị hàm số y = {x^2}\left| {x - 3} \right| tại 4 điểm phân biệt \Leftrightarrow 0 < m + \dfrac{1}{m} < 4 \Leftrightarrow \left\{ \begin{gathered} \dfrac{{{m^2} + 1}}{m} > 0 \hfill \\ \dfrac{{{m^2} - 4m + 1}}{m} < 0 \hfill \\ \end{gathered} \right. \begin{gathered} \Leftrightarrow \left\{ \begin{gathered} m > 0 \hfill \\ {m^2} - 4m + 1 < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m > 0 \hfill \\ 2 - \sqrt 3 < m < 2 + \sqrt 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}
\Leftrightarrow 2 - \sqrt 3 < m < 2 + \sqrt 3
Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} và có đồ thị như hình vẽ.
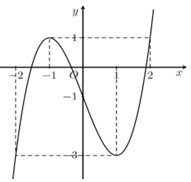
Có bao nhiêu giá trị nguyên của tham số m để phương trình f\left( {f\left( x \right) + m} \right) + 1 = f\left( x \right) + m có đúng 3 nghiệm phân biệt trên \left[ { - 1;1} \right].
Ta có: f\left( {f\left( x \right) + m} \right) + 1 = f\left( x \right) + m
Đặt t = f\left( x \right) + m, phương trình trở thành: f\left( t \right) + 1 = t \Leftrightarrow f\left( t \right) = t - 1\,\,\,\left( * \right).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f\left( t \right) và đường thẳng y = t - 1.
Vẽ đồ thị hàm số y = f\left( t \right) và đường thẳng y = t - 1 trên cùng một mặt phẳng tọa độ.
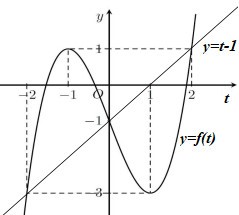
Dựa vào đồ thị hàm số ta thấy \left( * \right) \Leftrightarrow \left[ \begin{array}{l}t = - 2\\t = 0\\t = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = - m - 2\\f\left( x \right) = - m\\f\left( x \right) = - m + 2\end{array} \right..
Dựa vào đồ thị trên \left[ { - 1;1} \right], phương trình f\left( {f\left( x \right) + m} \right) + 1 = f\left( x \right) + m có đúng 3 nghiệm phân biệt khi và chỉ khi \left\{ \begin{array}{l} - 3 \le - m - 2 \le 1\\ - 3 \le - m \le 1\\ - 3 \le - m + 2 \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3 \le m \le 1\\ - 1 \le m \le 3\\1 \le m \le 5\end{array} \right. \Leftrightarrow m = 1.
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} và có bảng biến thiên như hình vẽ.
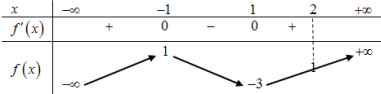
Có bao nhiêu giá trị nguyên của tham số m để phương trình f\left( {\left| {2f\left( x \right) + m} \right|} \right) = 1 có đúng 2 nghiệm trên \left[ { - 1;1} \right].
Ta có:
f\left( {\left| {2f\left( x \right) + m} \right|} \right) = 1 \Leftrightarrow \left[ \begin{array}{l}\left| {2f\left( x \right) + m} \right| = - 1\,\,\,\,\left( 1 \right)\\\left| {2f\left( x \right) + m} \right| = 2\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.
Phương trình (1) vô nghiệm.
Phương trình (2) \Leftrightarrow \left[ \begin{array}{l}2f\left( x \right) + m = 2\\2f\left( x \right) + m = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = \dfrac{{2 - m}}{2}\\f\left( x \right) = \dfrac{{ - 2 - m}}{2}\end{array} \right..
Dựa vào BBT trên \left[ { - 1;1} \right], để phương trình f\left( {\left| {2f\left( x \right) + m} \right|} \right) = 1 có đúng 2 nghiệm thì \left\{ \begin{array}{l} - 3 \le \dfrac{{2 - m}}{2} \le 1\\ - 3 \le \dfrac{{ - 2 - m}}{2} \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 8\\ - 4 \le m \le 4\end{array} \right. \Leftrightarrow 0 \le m \le 4.
Mà m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2;3;4} \right\}. Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Tìm m để phương trình 2{\left| x \right|^3} - 9{x^2} + 12\left| x \right| = m có 6 nghiệm phân biệt.
Số nghiệm của pt 2{\left| x \right|^3} - 9{x^2} + 12\left| x \right| = m là số giao điểm của đồ thị hàm số y = 2{\left| x \right|^3} - 9{x^2} + 12\left| x \right| và đường thẳng y = m.
Ta có đồ thị hàm số y = 2{\left| x \right|^3} - 9{x^2} + 12\left| x \right|:
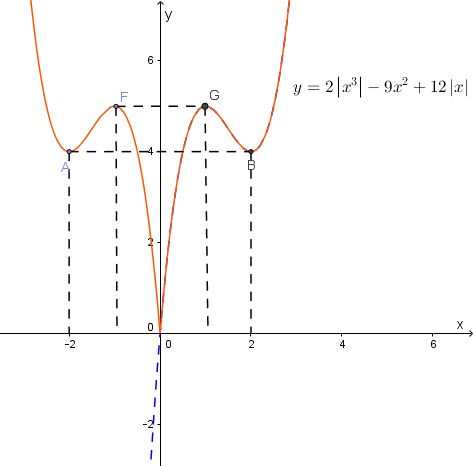
Pt 2{\left| x \right|^3} - 9{x^2} + 12\left| x \right| = m có 6 nghiệm phân biệt khi và chỉ khi đường thẳng y = m cắt đồ thị hàm số y = 2{\left| x \right|^3} - 9{x^2} + 12\left| x \right| tại 6 điểm phân biệt \Leftrightarrow 4 < m < 5.
Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} có bảng biến thiên như hình vẽ:
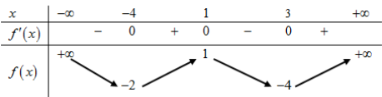
Số nghiệm của phương trình \left| {f\left( {f\left( x \right)} \right)} \right| = 2 là:
Ta có: \left| {f\left( {f\left( x \right)} \right)} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}f\left( {f\left( x \right)} \right) = 2\,\,\,\,\,\,\left( 1 \right)\\f\left( {f\left( x \right)} \right) = - 2\,\,\,\left( 2 \right)\end{array} \right.
\left( 1 \right) \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a < - 4\,\,\,\left( {1.1} \right)\\f\left( x \right) = b > 3\,\,\,\,\,\,\,\left( {1.2} \right)\end{array} \right., \left( 2 \right) \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = - 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {2.1} \right)\\f\left( x \right) = c \in \left( {1;3} \right)\,\,\,\left( {2.2} \right)\\f\left( x \right) = d > 3\,\,\,\,\,\,\,\,\,\,\left( {2.3} \right)\end{array} \right.
Tiếp tục dựa vào BBT ta có:
- Phương trình (1.1) có 0 nghiệm.
- Phương trình (1.2) có 2 nghiệm phân biệt.
- Phương trình (2.1) có 1 nghiệm.
- Phương trình (2.2) có 2 nghiệm phân biệt.
- Phương trình (2.3) có 2 nghiệm phân biệt.
Rõ ràng 7 nghiệm trên là phân biệt.
Vậy phương trình \left| {f\left( {f\left( x \right)} \right)} \right| = 2 có 7 nghiệm phân biệt.
Cho hàm số y = \dfrac{x}{{1 - x}}\,\,\left( C \right) và điểm A\left( { - 1;1} \right). Tìm m để đường thẳng d:\,\,y = mx - m - 1 cắt \left( C \right) tại 2 điểm phân biệt M,\,\,N sao cho A{M^2} + A{N^2} đạt giá trị nhỏ nhất.
Xét phương trình hoành độ giao điểm:.
\begin{array}{l}\,\,\,\,\,\,\dfrac{x}{{1 - x}} = mx - m - 1\,\,\left( {x \ne 1} \right)\\ \Leftrightarrow x = \left( {mx - m - 1} \right)\left( {1 - x} \right)\\ \Leftrightarrow x = mx - m - 1 - m{x^2} + mx + x\\ \Leftrightarrow m{x^2} - 2mx + m + 1 = 0\,\,\,\left( * \right)\end{array}
Để đường thẳng d:\,\,y = mx - m - 1 cắt \left( C \right) tại 2 điểm phân biệt M,\,\,N thì phương trình (*) phải có 2 nghiệm phân biệt khác 1 \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - m\left( {m + 1} \right) > 0\\m - 2m + m + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - m > 0\\1 \ne 0\end{array} \right. \Leftrightarrow m < 0.
Khi đó hoành độ của hai điểm M,\,\,N là nghiệm của phương trình (*), áp dụng định lí Vi-ét ta có: \left\{ \begin{array}{l}{x_M} + {x_N} = 2\\{x_M}.{x_N} = \dfrac{{m + 1}}{m}\end{array} \right..
Ta có: \left\{ \begin{array}{l}{y_M} = m{x_M} - m - 1\\{y_N} = m{x_N} - m - 1\end{array} \right. \Rightarrow {y_M} + {y_N} = \left( {{x_M} + {x_N}} \right) - 2m - 2 = - 2.
Gọi I là trung điểm của MN, ta có I\left( {1; - 1} \right) \Rightarrow A{I^2} = {2^2} + {\left( { - 2} \right)^2} = 8.
\begin{array}{l}M{N^2} = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {{y_M} - {y_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {m{x_M} - m - 1 - m{x_N} + m + 1} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{x_M} - {x_N}} \right)^2} + {m^2}{\left( {{x_M} - {x_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right){\left( {{x_M} - {x_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right)\left[ {{{\left( {{x_M} + {x_N}} \right)}^2} - 4{x_M}{x_N}} \right]\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right)\left[ {4 - 4\dfrac{{m + 1}}{m}} \right]\\\,\,\,\,\,\,\,\,\,\,\,\, = - 4\dfrac{{1 + {m^2}}}{m}\end{array}
Do M{N^2} > 0 nên m < 0.
Đặt T = A{M^2} + A{N^2}
Ta có:
\begin{array}{l}A{I^2} = \dfrac{{A{M^2} + A{N^2}}}{2} - \dfrac{{M{N^2}}}{4}\\ \Rightarrow 4A{I^2} = 2T - M{N^2}\\ \Leftrightarrow T = \dfrac{{4A{I^2} + M{N^2}}}{2} \Leftrightarrow T = \dfrac{{4.8 - 4\dfrac{{1 + {m^2}}}{m}}}{2}\\ \Leftrightarrow T = 16 - 2\dfrac{{1 + {m^2}}}{m} \Leftrightarrow T = \dfrac{{ - 2{m^2} + 16m - 2}}{m}\end{array}
Ta có:
\begin{array}{l}T' = \dfrac{{\left( { - 4m + 16} \right)m - \left( { - 2{m^2} + 16m - 2} \right)}}{{{m^2}}}\\T' = \dfrac{{ - 4{m^2} + 16m + 2{m^2} - 16m + 2}}{{{m^2}}}\\T' = \dfrac{{ - 2{m^2} + 2}}{{{m^2}}} = 0 \Leftrightarrow m = \pm 1\end{array}
BBT:
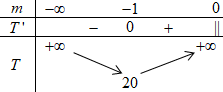
Từ BBT ta thấy \min T = 20 \Leftrightarrow m = - 1 .
Đề thi THPT QG - 2021 - mã 101
Đồ thị hàm số y = - {x^4} + 4{x^2} - 3 cắt trục tung tại điểm có tung độ bằng
Đồ thị hàm số y = - {x^4} + 4{x^2} - 3 cắt trục tung \Rightarrow x = 0
Với x = 0 thay vào hàm số \Rightarrow y = - 3.

