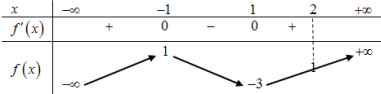
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.

Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {2f\left( x \right) + m} \right|} \right) = 1\) có đúng 2 nghiệm trên \(\left[ { - 1;1} \right]\).

Ta có:

\(f\left( {\left| {2f\left( x \right) + m} \right|} \right) = 1 \Leftrightarrow \left[ \begin{array}{l}\left| {2f\left( x \right) + m} \right| =  - 1\,\,\,\,\left( 1 \right)\\\left| {2f\left( x \right) + m} \right| = 2\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Phương trình (1) vô nghiệm.

Phương trình (2) \( \Leftrightarrow \left[ \begin{array}{l}2f\left( x \right) + m = 2\\2f\left( x \right) + m =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = \dfrac{{2 - m}}{2}\\f\left( x \right) = \dfrac{{ - 2 - m}}{2}\end{array} \right.\).

Dựa vào BBT trên \(\left[ { - 1;1} \right]\), để phương trình \(f\left( {\left| {2f\left( x \right) + m} \right|} \right) = 1\) có đúng 2 nghiệm thì \(\left\{ \begin{array}{l} - 3 \le \dfrac{{2 - m}}{2} \le 1\\ - 3 \le \dfrac{{ - 2 - m}}{2} \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 8\\ - 4 \le m \le 4\end{array} \right. \Leftrightarrow 0 \le m \le 4\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2;3;4} \right\}\). Vậy có 5 giá trị của \(m\) thỏa mãn yêu cầu bài toán.