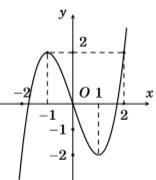
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Tổng tất cả giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt {2f\left( {\cos x} \right)} } \right) = m\) có nghiệm \(x \in \left[ {\dfrac{\pi }{2};\pi } \right)\) là:
Trả lời bởi giáo viên
Ta có: \( - 1 < \cos x \le 0\,\,\,\forall x \in \left[ {\dfrac{\pi }{2};\pi } \right)\), khi đó dựa vào đồ thị hàm số ta có \(0 \le f\left( {\cos x} \right) < 2\).
\( \Leftrightarrow 0 \le 2f\left( {\cos x} \right) < 4 \Leftrightarrow 0 \le \sqrt {2f\left( {\cos x} \right)} < 2\).
Đặt \(t = \sqrt {2f\left( {\cos x} \right)} \) \( \Rightarrow t \in \left[ {0;2} \right)\).
Khi đó yêu cầu bài toán trở thành: Tổng tất cả giá trị nguyên của tham số \(m\) để phương trình \(f\left( t \right) = m\) có nghiệm \(t \in \left[ {0;2} \right)\).
Dựa vào đồ thị hàm số ta thấy với \(t \in \left[ {0;2} \right)\) thì \(f\left( t \right) \in \left[ { - 2;2} \right)\), do đó phương trình \(f\left( t \right) = m\) có nghiệm \( \Leftrightarrow m \in \left[ { - 2;2} \right)\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1} \right\}\).
Vậy tổng các giá trị của \(m\) thỏa mãn là \( - 2 - 1 + 0 + 1 = - 2\).
Hướng dẫn giải:
- Tìm khoảng giá trị của \(f\left( {\cos x} \right)\) ứng với \(x \in \left[ {\dfrac{\pi }{2};\pi } \right)\).
- Đặt \(t = \sqrt {2f\left( {\cos x} \right)} \), xác định khoảng giá trị của \(t\).
- Đưa phương trình về dạng \(f\left( t \right) = m\), dựa vào đồ thị hàm số xác định các giá trị của \(m\) để phương trình có nghiệm \(t\) thuộc khoảng giá trị của nó xác định được ở phía trên.

