Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
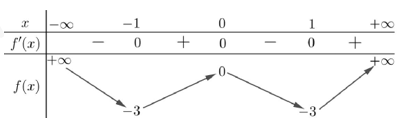
Phương trình \(f\left( {{x^2} - 1} \right) + 1 = 0\) có bao nhiêu nghiệm thực?
Đáp án
Đáp án
Bước 1: Đặt \(t = {x^2} - 1\) \( \Rightarrow t \ge - 1\). Đưa phương trình đã cho về phương trình ẩn \(t\).
Đặt \(t = {x^2} - 1\) \( \Rightarrow t \ge - 1\).
Phương trình đã cho trở thành \(f\left( t \right) + 1 = 0 \Leftrightarrow f\left( t \right) = - 1,\,\,t \ge - 1\,\,\,\left( * \right)\).
Bước 2: Biện luận số nghiệm của $x$
Dựa vào BBT ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại 3 điểm có hoành độ lớn hơn hoặc bằng \( - 1\).
Suy ra phương trình (*) có 3 nghiệm thực \(t\), ứng với mỗi nghiệm \(t\) cho 2 nghiệm thực \(x\).
Vậy phương trình đã cho có 6 nghiệm thực.
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới.
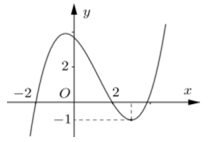
Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3}\) là
Đáp án
Đáp án
Bước 1: Đặt \(t = {x^3} - 3x\), quan sát đồ thị tìm nghiệm của phương trình \(\left| {f\left( t \right)} \right| = \dfrac{2}{3}\) tìm các nghiệm \({t_i}\).
Ta có :\(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3}\)\( \Leftrightarrow \left[ \begin{array}{l}f\left( {{x^3} - 3x} \right) = \dfrac{2}{3}\\f\left( {{x^3} - 3x} \right) = - \dfrac{2}{3}\end{array} \right.\)
Đặt \(t = {x^3} - 3x\) ta được \(\left[ \begin{array}{l}f\left( t \right) = \dfrac{2}{3}\\f\left( t \right) = - \dfrac{2}{3}\end{array} \right.\)
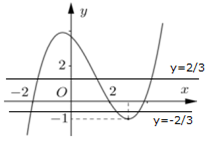
+) Phương trình \(f\left( t \right) = \dfrac{2}{3}\) có ba nghiệm phân biệt \({t_1},\,\,{t_2},\,\,{t_3}\), trong đó \( - 2 < {t_1} < 0 < {t_2} < 2 < {t_3}\).
+) Phương trình \(f\left( t \right) = - \dfrac{2}{3}\) có ba nghiệm phân biệt \({t_4},\,\,{t_5},\,\,{t_6}\), trong đó \({t_4} < - 2 < 2 < {t_5} < {t_6}\) .
Các nghiệm \({t_1},\,\,{t_2},\,\,{t_3},\,\,{t_4},\,\,{t_5},\,\,{t_6}\) phân biệt.
Bước 2: Khảo sát hàm số \(g\left( x \right) = {x^3} - 3x\) suy ra số nghiệm của phương trình \({x^3} - 3x = {t_i}\).
Xét hàm \(g\left( x \right) = {x^3} - 3x\) có \(g'\left( x \right) = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\)
BBT :
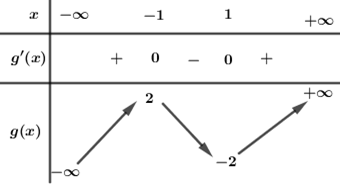
Từ BBT ta thấy :
+) Phương trình \({x^3} - 3x = {t_1} \in \left( { - 2;0} \right)\) có \(3\) nghiệm phân biệt.
+) Phương trình \({x^3} - 3x = {t_2} \in \left( {0;2} \right)\) có \(3\) nghiệm phân biệt.
+) Phương trình \({x^3} - 3x = {t_3} > 2\) có đúng \(1\) nghiệm.
+) Phương trình \({x^3} - 3x = {t_4} < - 2\) có đúng \(1\) nghiệm.
+) Phương trình \({x^3} - 3x = {t_5} > 2\) có đúng \(1\) nghiệm.
+) Phương trình \({x^3} - 3x = {t_6} > 2\) có đúng \(1\) nghiệm.
Vậy phương trình đã cho có tất cả \(3 + 3 + 1 + 1 + 1 + 1 = 10\) nghiệm.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ dưới đây.
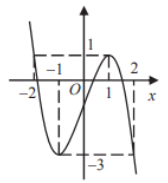
Hỏi phương trình \(f\left( {2 - f\left( x \right)} \right) = 1\) có tất cả bao nhiêu nghiệm thực phân biệt?
Đáp án:
Đáp án:
Dựa vào đồ thị ta có:
\(f\left( {2 - f\left( x \right)} \right) = 1 \Leftrightarrow \left[ \begin{array}{l}2 - f\left( x \right) = - 2\\2 - f\left( x \right) = 1\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 4\\f\left( x \right) = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = {x_0} \in \left( { - \infty ; - 2} \right)\\x = - 2\\x = 1\end{array} \right.\)
Vậy phương trình \(f\left( {2 - f\left( x \right)} \right) = 1\) có tất cả \(3\) nghiệm thực phân biệt.
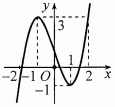
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( {\sqrt {4 - {x^2}} } \right) = m\) có nghiệm thuộc nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) là
Đáp án:
Đáp án:
Bước 1: Tính \(\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]'\) và tìm nghiệm của \(\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]' = 0\).
Xét hàm \(y = f\left( {\sqrt {4 - {x^2}} } \right)\) trên nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) ta có:
\(y' = {\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]^\prime }\) \( = {\left( {\sqrt {4 - {x^2}} } \right)^\prime }.f'\left( {\sqrt {4 - {x^2}} } \right)\) \( = \dfrac{{ - x.f'\left( {\sqrt {4 - {x^2}} } \right)}}{{\sqrt {4 - {x^2}} }}\)
\(y' = 0 \Leftrightarrow x.f'\left( {\sqrt {4 - {x^2}} } \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{f'\left( {\sqrt {4 - {x^2}} } \right)}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{\sqrt {4 - {x^2}} {\rm{\;}} = {\rm{\;}} - 1}\\{\sqrt {4 - {x^2}} {\rm{\;}} = 1}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = {\rm{\;}} \pm \sqrt 3 {\rm{\;}} \notin \left[ { - \sqrt 2 ;\sqrt 3 } \right)}\end{array}} \right. \Leftrightarrow x = 0\)
Bước 2: Lập bảng biến thiên của hàm số \(y = f\left( {\sqrt {4 - {x^2}} } \right)\) trên nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) rồi suy ra tập giá trị của \(m\).
Bảng biến thiên:
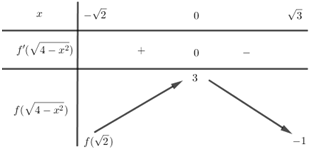
Từ đồ thị hàm số đã cho ta thấy \( - 1 < f\left( {\sqrt 2 } \right)\) nên để phương trình \(f\left( {\sqrt {4 - {x^2}} } \right) = m\) có nghiệm trong nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) thì \( - 1 < m \le 3\).
Vậy \(m \in \left( { - 1;3} \right]\).
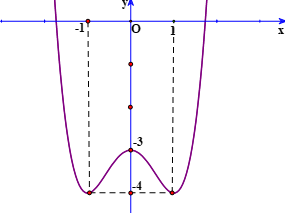
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có đúng hai nghiệm trên đoạn \(\left[ {0;\pi } \right]\).
Đáp án:
Đáp án:
Bước 1:
Đặt \(t = \sin x \in \left[ { - 1;1} \right]\).
Dễ thấy với mỗi \(t \in \left[ {0;1} \right)\) thì sẽ có 2 giá trị \(x \in \left[ {0;\pi } \right]\).
Bước 2:
Do đó, để phương trình đã cho có đúng hai nghiệm trên đoạn \(\left[ {0;\pi } \right]\) thì phương trình \(f\left( t \right) = m\) có nghiệm duy nhất \(t \in \left[ {0;1} \right)\)\( \Leftrightarrow - 4 < m \le - 3\).
Vậy có đúng 1 giá trị nguyên của m thỏa mãn bài toán.
