Cho hình chóp tứ giác đều có cạnh đáy dài $16cm$ và trung đoạn dài $20cm.$ Tính thể tích hình chóp. (làm tròn đến hàng phần trăm)
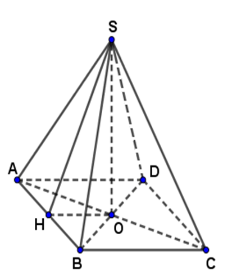
Xét hình chóp tứ giác đều $S.ABCD\;$ có đáy là hình vuông cạnh $16cm$.
$SO$ là đường cao; $SH$ là trung đoạn $(H \in AB)$
Vì $SAB$ là tam giác cân nên $H$ là trung điểm của $AB$.
$O$ là giao điểm của hai đường chéo trong hình vuông $ABCD$ nên $O$ là trung điểm $AC$
Do đó, $HO$ là đường trung bình trong tam giác $ABC,$ suy ra $HO = \dfrac{1}{2}BC = 8(cm)$
Xét tam giác $SHO$ vuông tại $O,$
Áp dụng định lý Pytago, ta có:
$S{H^2} = H{O^2} + S{O^2}$$ \Rightarrow SO^2 = S{H^2} - H{O^2}$ $ \Rightarrow SO = \sqrt {400 - 64} = 4\sqrt {21} (cm)$
Vậy thể tích hình chóp $S.ABCD\;$ là
$V=\dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.4\sqrt {21} {.16^2} \approx 1564,19\,\left( {c{m^3}} \right)$
Cho hình chóp tam giác đều $S.ABC$ có tất cả các cạnh bằng $2{\rm{ }}dm.$ Tính độ dài đoạn thẳng $MN$ nối trung điểm 2 cạnh đối $AB$ và $SC.$
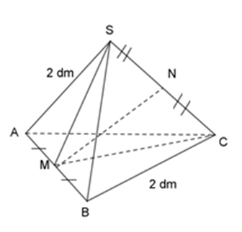
Theo đề bài ta có:
\(\begin{array}{l}AM = MB = \dfrac{1}{2}AB = 1\;dm\\SN = NC = \dfrac{1}{2}SC = 1\;dm\end{array}\)
Ta có $CM$ là đường trung tuyến của tam giác $ABC.$
Vì tam giác $ABC$ là tam giác đều nên $CM$ cũng là đường cao của tam giác $ABC.$
Áp dụng định lý Pitago vào tam giác $CMB$ vuông tại $M:$
\(\begin{array}{l}M{C^2} + M{B^2} = B{C^2}\\ \Leftrightarrow M{C^2} = B{C^2} - M{B^2} = {2^2} - 1 = 3\\ \Rightarrow MC = \sqrt 3 \;dm\end{array}\)
Tương tự ta xét tam giác vuông $SMB,$ ta tính được: \(SM = \sqrt 3 \;dm\)
Xét tam giác $SMC$ có: \(M{\rm{S}} = MC = \sqrt 3 \;dm\)
\( \Rightarrow \) Tam giác $SMC$ là tam giác cân tại $M.$
\( \Rightarrow \) MN vừa là đường trung tuyến vừa là đường cao của tam giác SMC.
Áp dụng định lý Pitago cho tam giác MNC vuông tại N:
\(\begin{array}{l}M{N^2} + N{C^2} = M{C^2}\\ \Leftrightarrow M{N^2} = M{C^2} - N{C^2} = 3 - 1 = 2\\ \Rightarrow MN = \sqrt 2 \;dm\end{array}\)
Cho hình chóp cụt đều có 2 đáy là các hình vuông cạnh a và 2a, trung đoạn bằng a. Tính diện tích xung quanh của hình chóp cụt đều?
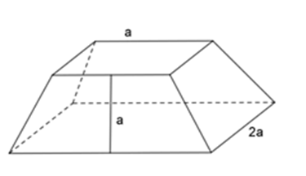
Hình chóp cụt đều có 4 mặt bên là các hình thang cân bằng nhau.
Suy ra, diện tích xung quanh của hình chóp cụt đều là tổng diện tích 4 hình thang cân, khi đó diện tích một mặt bên là $S=\dfrac{(a+2a).a}{2}=\dfrac{3a^2}{2}$
Diện tích xung quanh hình chóp cụt đều là
\({S_{xq}} = 4. \dfrac{3a^2}{2}= 6{{\rm{a}}^2}\)
Cho hình chóp tứ giác đều $S.ABCD$ , đáy $ABCD$ là hình vuông có cạnh $3{\rm{ }}cm,$ cạnh bên $SB$ bằng $5{\rm{ }}cm.$
Tính bình phương đường cao $SH$ của hình chóp.
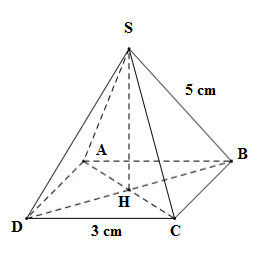
Lấy H là giao của 2 đường chéo hình vuông $AC$ và $BD,$ khi đó ta có $SH$ là đường cao của hình chóp đều.
+) Áp dụng định lý Pitago cho tam giác $ABC$ vuông tại $B:$
\(\begin{array}{l}\;\;\;\;A{B^2} + B{C^2} = A{C^2}\\ \Leftrightarrow A{C^2} = {3^2} + {3^2} = 18\\ \Rightarrow AC = \sqrt {18} = 3\sqrt 2 \;cm\end{array}\)
\( \Rightarrow HC = \dfrac{1}{2}AC = \dfrac{1}{2}.3\sqrt 2 = \dfrac{{3\sqrt 2 }}{2}\;cm\) (Vì H là trung điểm AC)
Áp dụng định lý Pitago cho tam giác SHC vuông tại H có:
\(\begin{array}{l}\;\;\;\;S{H^2} + H{C^2} = S{C^2}\\ \Leftrightarrow S{H^2} = S{C^2} - H{C^2} = {5^2} - {\left( {\dfrac{{3\sqrt 2 }}{2}} \right)^2} = \dfrac{{82}}{4} = \dfrac{{41}}{2}\end{array}\)
Vậy \(S{H^2} = \dfrac{{41}}{2}.\)
Cho hình chóp tứ giác đều $S.ABCD$ , đáy $ABCD$ là hình vuông có cạnh $3{\rm{ }}cm,$ cạnh bên $SB$ bằng $5{\rm{ }}cm.$
Tính diện tích xung quanh hình chóp
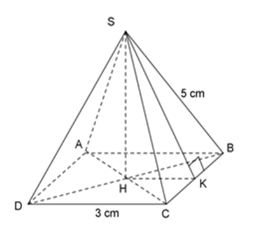
+ Kẻ $SK$ vuông góc với $BC$ (\(K \in BC\))
+ Vì tam giác $SBC$ là tam giác cân tại $S$ nên $SK$ vừa là đường cao vừa là đường trung tuyến.
\( \Rightarrow CK = KB = \dfrac{1}{2}BC = \dfrac{3}{2}\;cm\)
Áp dụng định lý Pitago cho tam giác $SKB$ vuông tại $K:$
\(\begin{array}{l}\;\;\;S{K^2} + K{B^2} = S{B^2}\\ \Leftrightarrow S{K^2} = S{B^2} - K{B^2} = {5^2} - {\left( {\dfrac{3}{2}} \right)^2} = \dfrac{{91}}{4}\\ \Rightarrow SK = \dfrac{{\sqrt {91} }}{2}\;cm.\end{array}\)
Vậy diện tích xung quanh của hình chóp đều $S.ABCD$ là: \({S_{xq}} =4.S_{SBC}= 4.\dfrac{1}{2}.BC.SK\)\(=4.\dfrac{1}{2}.3.\dfrac{{\sqrt {91} }}{2} = 3\sqrt {91} \;c{m^2}\)
Cho hình hộp chữ nhật $ABCD.EFGH.$ Chọn câu đúng:
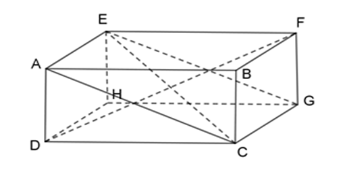
+ ) Ta có:\(\) \(AE//CG,\;A{\rm{E}} = CG\;(gt)\)
Suy ra tứ giác ACGE là hình bình hành.
Mặt khác: \(A{\rm{E}} \bot mp(EFGH)\)
Mà \(EG \subset mp(EFGH) \Rightarrow AE \bot EG\;\)tại $E.$
Vậy tứ giác $ACGE$ là hình chữ nhật nên $A$ đúng.
+) Vì \(DH \bot mp(EFGH)\) nên \(DH \bot HF\) tại $H.$
Áp dụng định lý Pitago cho tam giác $DHF$ vuông tại $H,$ ta có: \(D{H^2} + H{F^2} = D{F^2}\;(1)\)
Vì \(A{\rm{E}} \bot mp(ABC{\rm{D}})\) nên \(A{\rm{E}} \bot AC\) tại $A.$
Áp dụng định lý Pitago cho tam giác EAC vuông tại A, ta có: \(E{{\rm{A}}^2} + A{C^2} = E{C^2}\;(2)\)
Mà DH = AE; HF = EG = AC (Hai đường chéo của hình chữ nhật) (3)
Từ (1), (2), (3) suy ra: \(D{F^2} = E{C^2} \Rightarrow DF = CE\;\)nên B đúng.
Cho hình hộp chữ nhật $ABCD.A'B'C'D' .$ Tính diện tích hình chữ nhật $ADC'B' \;$ biết $AB = 28cm,B' {D^2} = 3709,DD' = 45cm.$
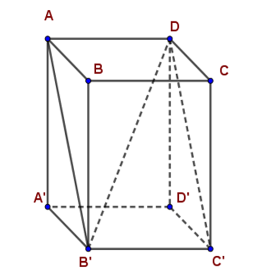
Xét tam giác $AA' B'$ vuông tại $A' $ có: $AA' = DD' = 45cm$ và $A' B' = AB = 28cm$
Áp dụng định lý Pytago ta có:
$AA'^2 + A'B'^2 = AB'^2 $$\Leftrightarrow AB'= \sqrt {AA'^2 + A' B'^2}= 53cm$
Ta có: $AD \bot AA' ;AD \bot AB$ suy ra $AD \bot mp(AA' B' B) \Rightarrow AD \bot AB' $
Xét tam giác $ADB' $ vuông tại $A$ có: $AB' = 53cm$ và $DB'^2 = 3709$
Áp dụng định lý Pytago ta có:
$A{D^2} + AB'^2 = DB'^2 \Leftrightarrow AD = \sqrt {DB'^2 - AB'^2} $ \( = \sqrt {3709 - {{53}^2}} = 30\,cm\)
Vậy diện tích $ADC' B' $ bằng $AD.AB' = 30.53 = 1590(c{m^2})$

