Cho hình chóp tứ giác đều $S.ABCD$ , đáy $ABCD$ là hình vuông có cạnh $3{\rm{ }}cm,$ cạnh bên $SB$ bằng $5{\rm{ }}cm.$

Tính diện tích xung quanh hình chóp

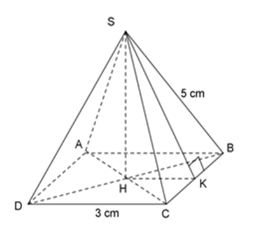
+ Kẻ $SK$ vuông góc với $BC$ (\(K \in BC\))

+ Vì tam giác $SBC$  là tam giác cân tại $S$ nên $SK$ vừa là đường cao vừa là đường trung tuyến.

\( \Rightarrow CK = KB = \dfrac{1}{2}BC = \dfrac{3}{2}\;cm\)

Áp dụng định lý Pitago cho tam giác $SKB$ vuông tại $K:$

\(\begin{array}{l}\;\;\;S{K^2} + K{B^2} = S{B^2}\\ \Leftrightarrow S{K^2} = S{B^2} - K{B^2} = {5^2} - {\left( {\dfrac{3}{2}} \right)^2} = \dfrac{{91}}{4}\\ \Rightarrow SK = \dfrac{{\sqrt {91} }}{2}\;cm.\end{array}\)

Vậy diện tích xung quanh của hình chóp đều $S.ABCD$ là: \({S_{xq}} =4.S_{SBC}= 4.\dfrac{1}{2}.BC.SK\)\(=4.\dfrac{1}{2}.3.\dfrac{{\sqrt {91} }}{2} = 3\sqrt {91} \;c{m^2}\)