Cho hình chóp tứ giác đều $S.ABCD$ , đáy $ABCD$ là hình vuông có cạnh $3{\rm{ }}cm,$ cạnh bên $SB$ bằng $5{\rm{ }}cm.$

Tính bình phương đường cao $SH$ của hình chóp.

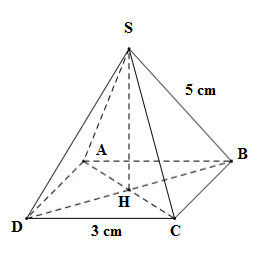
Lấy H là giao của 2 đường chéo hình vuông $AC$ và $BD,$ khi đó ta có $SH$ là đường cao của hình chóp đều.

+) Áp dụng định lý Pitago cho tam giác $ABC$ vuông tại $B:$

\(\begin{array}{l}\;\;\;\;A{B^2} + B{C^2} = A{C^2}\\ \Leftrightarrow A{C^2} = {3^2} + {3^2} = 18\\ \Rightarrow AC = \sqrt {18}  = 3\sqrt 2 \;cm\end{array}\)

\( \Rightarrow HC = \dfrac{1}{2}AC = \dfrac{1}{2}.3\sqrt 2  = \dfrac{{3\sqrt 2 }}{2}\;cm\) (Vì H là trung điểm AC)

Áp dụng định lý Pitago cho tam giác SHC vuông tại H có:

\(\begin{array}{l}\;\;\;\;S{H^2} + H{C^2} = S{C^2}\\ \Leftrightarrow S{H^2} = S{C^2} - H{C^2} = {5^2} - {\left( {\dfrac{{3\sqrt 2 }}{2}} \right)^2} = \dfrac{{82}}{4} = \dfrac{{41}}{2}\end{array}\)

Vậy \(S{H^2} = \dfrac{{41}}{2}.\)