Cho hình chóp tam giác đều $S.ABC$ có tất cả các cạnh bằng $2{\rm{ }}dm.$ Tính độ dài đoạn thẳng $MN$ nối trung điểm 2 cạnh đối $AB$ và $SC.$

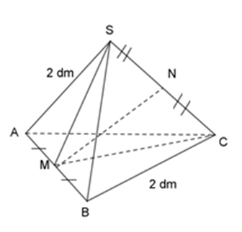
Theo đề bài ta có:

\(\begin{array}{l}AM = MB = \dfrac{1}{2}AB = 1\;dm\\SN = NC = \dfrac{1}{2}SC = 1\;dm\end{array}\)

Ta có $CM$ là đường trung tuyến của tam giác $ABC.$

Vì tam giác $ABC$ là tam giác đều nên $CM$ cũng là đường cao của tam giác $ABC.$

Áp dụng định lý Pitago vào tam giác $CMB$ vuông tại $M:$

\(\begin{array}{l}M{C^2} + M{B^2} = B{C^2}\\ \Leftrightarrow M{C^2} = B{C^2} - M{B^2} = {2^2} - 1 = 3\\ \Rightarrow MC = \sqrt 3 \;dm\end{array}\)

Tương tự ta xét tam giác vuông $SMB,$ ta tính được: \(SM = \sqrt 3 \;dm\)

Xét tam giác $SMC$ có: \(M{\rm{S}} = MC = \sqrt 3 \;dm\)

\( \Rightarrow \) Tam giác $SMC$ là tam giác cân tại $M.$

\( \Rightarrow \) MN vừa là đường trung tuyến vừa là đường cao của tam giác SMC.

Áp dụng định lý Pitago cho tam giác MNC vuông tại N:

\(\begin{array}{l}M{N^2} + N{C^2} = M{C^2}\\ \Leftrightarrow M{N^2} = M{C^2} - N{C^2} = 3 - 1 = 2\\ \Rightarrow MN = \sqrt 2 \;dm\end{array}\)