Hãy chọn câu trả lời đúng. Nếu tam giác $ABC$ đồng dạng với tam giác \(A'B'C'\) theo tỉ số $k$ thì tỉ số chu vi của hai tam giác đó bằng
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) theo tỉ số \(k\) nên \(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = k\) .
Ta có \(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}} = \dfrac{{{P_{ABC}}}}{{{P_{A'B'C'}}}} = k\).
Vậy tỉ số chu vi của hai tam giác là \(k\) .
Nếu tam giác $ABC$ có $MN$ // $BC$ (với \(M\in AB, N\in AC)\) thì
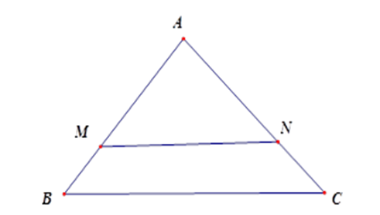
Vì \(MN{\rm{//}}BC \Rightarrow \) tam giác \(AMN\) đồng dạng với tam giác \(\Delta ABC\) .
Hãy chọn câu đúng. Hai \({\rm{\Delta }}ABC\) và \({\rm{\Delta }}DEF\) có \(\widehat A = {80^0},\widehat B = {70^0},\)\(\widehat F = {30^0};\,BC = 6\,cm.\) Nếu \({\rm{\Delta }}ABC\) đồng dạng với \({\rm{\Delta }}DEF\) thì:
Vì tam giác \(ABC\) đồng dạng với tam giác $DEF$ nên
\(\widehat A = \widehat D = 80^\circ ;\,\widehat B = \widehat E = 70^\circ ;\,\\\widehat C = \widehat F = 30^\circ \)
Vậy \(\widehat C = {30^0}\) là đúng.
Hãy chọn câu đúng. Tam giác $ABC$ đồng dạng với tam giác $MNP$ theo tỉ số \(\dfrac{2}{3}\), biết chu vi của tam giác $ABC$ bằng $40\,cm$ . Chu vi của tam giác $MNP$ là:
Vì tam giác $ABC$ đồng dạng với tam giác $MNP$ theo tỉ số \(\dfrac{2}{3}\) nên
\(\dfrac{{AB}}{{MN}} = \dfrac{{AC}}{{MP}} = \dfrac{{BC}}{{NP}} = \dfrac{{AB + AC + BC}}{{MN + MP + NP}} = \dfrac{{{P_{\Delta ABC}}}}{{{P_{\Delta MNP}}}}\) và \(\dfrac{{AB}}{{MN}} = \dfrac{2}{3} \Rightarrow \dfrac{{{P_{\Delta ABC}}}}{{{P_{\Delta MNP}}}} = \dfrac{2}{3}\)
Từ đó \({P_{\Delta MNP}} = \dfrac{{3.{P_{\Delta ABC}}}}{2} \)\(= \dfrac{{3.40}}{2} = 60\,cm.\)
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng
\(\Delta ABD\) và \(\Delta BDC\).
Chọn câu đúng nhất.
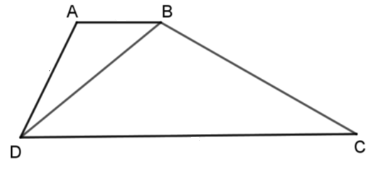
Vì \(\Delta ABD\)\(\backsim\)\(\Delta BDC\) (gt) nên \(\widehat {ABD} = \widehat {BDC}\) (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên \(AB\,{\rm{//}}\,CD\) suy ra \(ABCD\) là hình thang (dấu hiệu nhận biết).
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng
\(\Delta ABD\) và \(\Delta BDC\).
Tính các độ dài $BD$, $BC$ biết $AB = 2cm$ , $AD = 3cm$ ,$CD = 8cm$ .
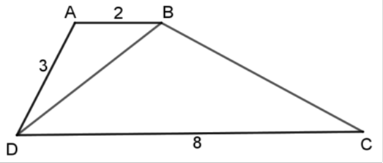
Vì \(\Delta ABD\)\(\backsim\)\(\Delta BDC\) nên
\(\dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{BC}},\) tức là
\(\dfrac{2}{{BD}} = \dfrac{{BD}}{8} = \dfrac{3}{{BC}}.\)
Ta có \(B{D^2} = 2.8 = 16\) nên \(BD = 4cm.\)
Suy ra \(BC = \dfrac{{8.3}}{4} = 6\,\left( {cm} \right).\)
Vậy \(BD = 4\,cm;BC = 6\,cm\) .
Hình thang ABCD (AB // CD) có AB = 10cm, CD = 25cm, hai đường chéo cắt nhau tại O.
Chọn khẳng định đúng.
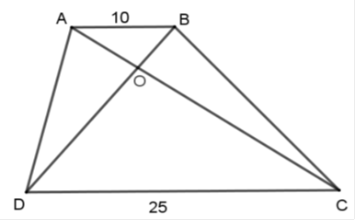
\(AB{\rm{//}}CD\) nên \(\Delta AOB\)\(\backsim\)\(\Delta COD.\) Tỉ số đồng dạng \(\dfrac{{AO}}{{OC}} = \dfrac{{BO}}{{OD}} = \dfrac{{AB}}{{CD}} = \dfrac{{10}}{{25}} = \dfrac{2}{5}.\)
Cho tam giác $ABC$ , điểm $M$ thuộc cạnh $BC$ sao cho \(\dfrac{{MB}}{{MC}} = \dfrac{1}{2}.\) Đường thẳng đi qua M và song song với $AC$ cắt $AB$ ở $D$ . Đường thẳng đi qua $M$ và song song với $AB$ cắt $AC$ ở $E$ . Biết chu vi tam giác $ABC$ bằng \(30\,cm\) . Chu vi của các tam giác $DBM$ và $EMC$ lần lượt là
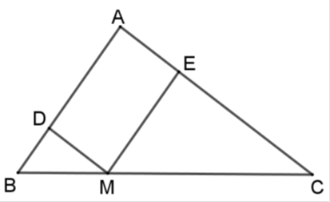
Ta có $MD$ // $AC$ nên \(\Delta DBM\)\(\backsim\)\(\Delta ABC\). Suy ra
\(\dfrac{{DB}}{{AB}} = \dfrac{{BM}}{{BC}} = \dfrac{{DM}}{{AC}} = \dfrac{{DB + BM + DM}}{{AB + BC + AC}}\)
Do đó \(\dfrac{1}{3} = \dfrac{{{P_{\Delta BDM}}}}{{{P_{\Delta ABC}}}}.\)
Chu vi \(\Delta DBM\) bằng \(30 \cdot \dfrac{1}{3} = 10\,\left( {cm} \right).\)
Ta có $ME$ // $AB$ nên \(\Delta EMC\)\(\backsim\)\(\Delta ABC.\) Suy ra
\(\dfrac{{EM}}{{AB}} = \dfrac{{MC}}{{BC}} = \dfrac{{EC}}{{AC}} = \dfrac{{EM + MC + EC}}{{AB + BC + AC}},\) do đó \(\dfrac{2}{3} = \dfrac{{{P_{\Delta {\rm E}{\rm M}C}}}}{{{P_{\Delta ABC}}}}.\)
Chu vi \(\Delta EMC\) bằng \(30 \cdot \dfrac{2}{3} = 20\,\left( {cm} \right).\)
Vậy chu vi \(\Delta DBM\) và chu vi \(\Delta EMC\) lần lượt là \(10\,cm;\,20\,cm\) .
Cho hình bình hành $ABCD$ . Trên đường chéo $AC$ lấy điểm $E$ sao cho $AC = 3AE$ . Qua $E$ vẽ đường thẳng song song với $CD$ , cắt $AD$ và $BC$ theo thứ tự ở $M$ và $N$ . Cho các khẳng định sau:
(I) \(\Delta AME\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \( k{ _1} = \dfrac{1}{3}.\)
(II) \(\Delta CBA\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng bằng \({k_2} = 1\) .
(III) \(\Delta CNE\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \({k_3} = \dfrac{2}{3}.\)
Chọn câu đúng.
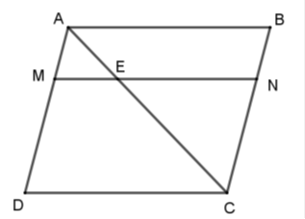
Vì \(ABCD\) là hình bình hành nên $ME$ // $DC$ và $EN$ // $AB$.
+ $ME$ // $DC$ nên \(\Delta AME\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \(\dfrac{{AE}}{{AC}} = \dfrac{1}{3}.\)
+ Vì \(ABCD\) là hình bình hành nên \(\widehat B = \widehat D;\,AD = BC;\,AB = DC \)\(\Rightarrow \) \(\Delta CBA = \Delta ADC\) nên
\(\Delta CBA\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng bằng $1$ .
+ $EN$ // $AB$ nên \(\Delta CNE\)\(\backsim\)\(\Delta CBA,\)do đó \(\Delta CNE\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \(\dfrac{{CE}}{{AC}} = \dfrac{2}{3}.\)
Vậy cả (I), (II), (III) đều đúng.

