Câu hỏi:
2 năm trước
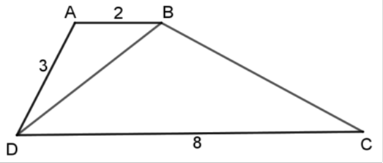
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng
\(\Delta ABD\) và \(\Delta BDC\).
Tính các độ dài $BD$, $BC$ biết $AB = 2cm$ , $AD = 3cm$ ,$CD = 8cm$ .
Trả lời bởi giáo viên
Đáp án đúng: d
Vì \(\Delta ABD\)\(\backsim\)\(\Delta BDC\) nên
\(\dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{BC}},\) tức là
\(\dfrac{2}{{BD}} = \dfrac{{BD}}{8} = \dfrac{3}{{BC}}.\)
Ta có \(B{D^2} = 2.8 = 16\) nên \(BD = 4cm.\)
Suy ra \(BC = \dfrac{{8.3}}{4} = 6\,\left( {cm} \right).\)
Vậy \(BD = 4\,cm;BC = 6\,cm\) .
Hướng dẫn giải:
Sử dụng các cạnh tương ứng tỉ lệ của hai tam giác đồng dạng và giả thiết để tính toán.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
