Câu hỏi:
2 năm trước
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng
\(\Delta ABD\) và \(\Delta BDC\).
Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: d
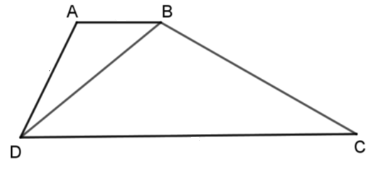
Vì \(\Delta ABD\)\(\backsim\)\(\Delta BDC\) (gt) nên \(\widehat {ABD} = \widehat {BDC}\) (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên \(AB\,{\rm{//}}\,CD\) suy ra \(ABCD\) là hình thang (dấu hiệu nhận biết).
Hướng dẫn giải:
+ Sử dụng các góc tương ứng bằng nhau của hai tam giác đồng dạng để chứng minh cặp góc so le trong bằng nhau.
+ Từ đó suy ra cặp cạnh song song và suy ra \(ABCD\) là hình thang.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
