Cho $\Delta ABC$ cân tại $A$ , có $BC = 2a$ , $M$ là trung điểm $BC$ , lấy $D,E$ thuộc $AB,AC$ sao cho \(\widehat {DME} = \widehat {ABC}\).
Tích $BD.CE$ bằng
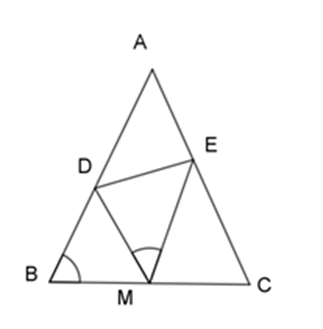
+ Ta có: \(\widehat {DMC} = \widehat {DME} + \widehat {EMC}\)
Mặt khác: \(\widehat {DMC} = \widehat {ABC} + \widehat {BDM}\) (góc ngoài tam giác)
Mà: \(\widehat {DME} = \widehat {ABC}\)(gt) nên \(\widehat {BDM} = \widehat {EMC}\)
+ Ta có: \(\widehat {ABC} = \widehat {ACB}\) ($\Delta ABC$ cân tại $A$ ) và \(\widehat {BDM} = \widehat {EMC}\) (chứng minh trên)
\( \Rightarrow \)\(\Delta BDM\backsim\Delta CME\;(g - g)\)
\( \Rightarrow \dfrac{{BD}}{{CM}} = \dfrac{{BM}}{{CE}} \Rightarrow BD.CE = CM.BM\)
Lại có M là trung điểm của BC và BC = 2a \( \Rightarrow \)BM = MC = a
\( \Rightarrow BD.CE = {a^2}\) không đổi.
Cho $\Delta ABC$ cân tại $A$ , có $BC = 2a$ , $M$ là trung điểm $BC$ , lấy $D,E$ thuộc $AB,AC$ sao cho \(\widehat {DME} = \widehat {ABC}\).
Góc \(BDM\) bằng với góc nào dưới đây?
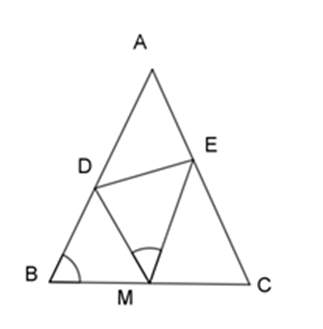
Ta có: \(\Delta BDM\backsim\Delta CME\;\) (chứng minh trên)
\( \Rightarrow \dfrac{{DM}}{{ME}} = \dfrac{{BD}}{{CM}} = \dfrac{{BD}}{{BM}}\) (do CM = BM (gt))
\( \Rightarrow \dfrac{{BD}}{{DM}} = \dfrac{{BM}}{{ME}}\)
Xét \(\Delta BDM\) và \(\Delta MDE\) ta có:
\(\dfrac{{BD}}{{DM}} = \dfrac{{BM}}{{ME}}\)
\(\widehat {DME} = \widehat {ABC}\) (gt)
\( \Rightarrow \Delta BDM\backsim\Delta MDE\;(c - g - c)\)
\( \Rightarrow \widehat {BDM} = \widehat {MDE}\) (hai góc tương ứng)

