Diện tích hình trụ, thể tích khối trụ
Kỳ thi ĐGNL ĐHQG Hà Nội
Cho hình vuông $ABCD$ có cạnh bằng $a$. Gọi $M,N$ lần lượt là trung điểm của $AB$ và $CD$. Khi quay hình vuông $ABCD$ quanh $MN$ tạo thành một hình trụ. Gọi $\left( S \right)$ là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu $\left( S \right)$ là:
Mặt trụ tạo bởi hình vuông $ABCD$ khi quay quanh $MN$ có chiều cao $h = a$ và bán kính đáy $r = \dfrac{a}{2}$ nên có diện tích toàn phần:
${S_{tp}} = 2\pi r\left( {r + h} \right) = 2\pi .\dfrac{a}{2}\left( {\dfrac{a}{2} + a} \right) = \dfrac{{3{a^2}\pi }}{2}$
Mặt cầu $\left( S \right)$ có diện tích bằng ${S_{tp}}$ của mặt trụ thì có bán kính $R$ với:
$4\pi {R^2} = \dfrac{{3{a^2}\pi }}{2} \Leftrightarrow R = \dfrac{{a\sqrt 6 }}{4}$
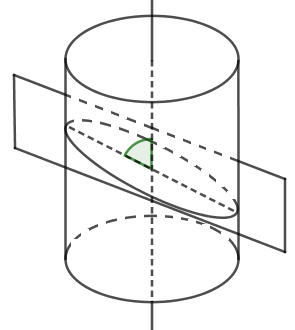
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) thì ta được:
Khi cắt mặt trụ bởi mặt phẳng tạo với trục một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) thì ta được elip.
Một hình trụ có chiều cao bằng $3$, chu vi đáy bằng $4\pi $. Thể tích của khối trụ là:
Bán kính đáy: \(r = \dfrac{C}{{2\pi }} = \dfrac{{4\pi }}{{2\pi }} = 2\)
Thể tích của khối trụ: $V = \pi {r^2}h = \pi {.2^2}.3 = 12\pi $.
Cho hình trụ có trục \(\Delta \) và bán kính \(R\). Khi cắt hình trụ bởi mặt phẳng \(\left( \alpha \right)\) song song với \(\Delta \) và cách \(\Delta \) một khoảng \(d\left( {\Delta ;\left( \alpha \right)} \right) = k < R\) thì ta được thiết diện là:
Khi cắt hình trụ bởi mặt phẳng song song với trục mà khoảng cách giữa \(\left( \alpha \right)\) và trục nhỏ hơn bán kính hình trụ thì ta được thiết diện là hình chữ nhật.
Tính thể tích \(V\) của khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$.
Khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$ thì bán kính đáy \(r = \dfrac{{a\sqrt 2 }}{2}\) và chiều cao \(h = a\).
Suy ra \(V = \pi {r^2}h = \dfrac{{\pi {a^3}}}{2}\)
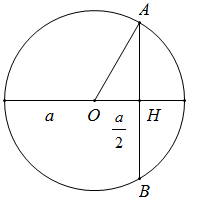
Cho hình trụ có bán kính đáy bằng \(a\). Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng \(\dfrac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích khối trụ.
Gọi $\left( O \right)$ là một đường tròn đáy của hình trụ
Mặt phẳng đã cho cắt $\left( O \right)$ tại $A$ và $B$, gọi $H$ là trung điểm $AB$.
Vì thiết diện thu được là hình vuông nên chiều cao hình trụ bằng
$h = AB = 2AH = 2\sqrt {O{A^2} - O{H^2}} = a\sqrt 3 $
Thể tích khối trụ là
$V = \pi {R^2}h = \pi {a^2}.a\sqrt 3 = \pi {a^3}\sqrt 3 $
Xét hình trụ \(T\) có thiết diện qua trục của hình trụ là hình vuông cạnh $a$. Tính diện tích toàn phần \(S\) của hình trụ.
Ta có: \(r = OA = \dfrac{{AB}}{2} = \dfrac{a}{2};h = AA' = a\) nên \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi .\dfrac{a}{2}.a + 2\pi .{\left( {\dfrac{a}{2}} \right)^2} = \pi {a^2} + \dfrac{{\pi {a^2}}}{2} = \dfrac{{3\pi {a^2}}}{2}\)
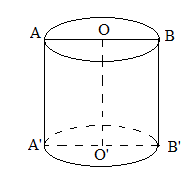
Cho hình trụ có các đáy là hình tròn tâm $O$ và tâm $O'$ , bán kính đáy bằng chiều cao và bằng $4cm$. Trên đường tròn đáy tâm $O$ lấy điểm $A$, trên đường tròn đáy tâm $O'$ lấy điểm B sao cho $AB = 4\sqrt 3 cm$. Thể tích khối tứ diện $AOO'B$ là:
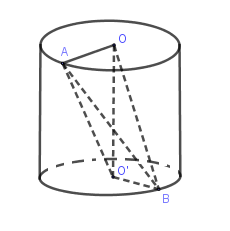
Tam giác \(OAO'\) vuông tại \(O\) nên:
\(O'A = \sqrt {O{A^2} + O'{O^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \)
Tam giác \(AO'B\) có:
\(O'{A^2} + O'{B^2} = A{B^2}\) nên tam giác \(AO'B\) vuông tại \(O'\)
Ta có $\left\{ \begin{array}{l}O'B \bot {\rm{OO'}}\\O'B \bot A{\rm{O'}}\end{array} \right. \Rightarrow O'B \bot \left( {{\rm{AOO'}}} \right)$
${S_{\Delta AOO'}} = \dfrac{1}{2}OA.OO= \dfrac{1}{2}.4.4 = 8$
$ \Rightarrow {V_{AOO'B}} = \dfrac{1}{3}{S_{\Delta AOO'}}.O'B = \dfrac{1}{3}.8.4 = \dfrac{{32}}{3}$
Một khối đồ chơi gồm hai khối trụ \(\left( {{H_1}} \right),\,\,\left( {{H_2}} \right)\) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là \({r_1},\,\,{h_1},\,\,{r_2},\,\,{h_2}\) thỏa mãn \({r_2} = \dfrac{1}{2}{r_1},\,\,{h_2} = 2{h_1}\) (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng \(30c{m^3}\) . Tính thể tích khối trụ \(\left( {{H_1}} \right)\) bằng:
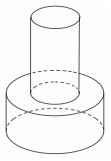
Thể tích của toàn bộ khối đồ chơi là:
\(\begin{array}{l}V = \pi r_1^2{h_1} + \pi r_2^2{h_2} = \pi r_1^2{h_1} + \pi \dfrac{1}{4}r_1^2.2{h_1} = \dfrac{3}{2}\pi r_1^2{h_1} = 30\\ \Rightarrow \pi r_1^2{h_1} = 20\end{array}\)
Vậy thể tích khối trụ (H1) là 20 cm3.
Người ta xếp hai quả cầu có cùng bán kính \(r\) vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là \(120\,\,c{m^3}\), thể tích của mỗi khối cầu bằng
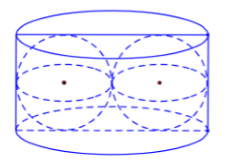
Dựa vào dữ kiện bài toán và hình vẽ \( \Rightarrow \) Hình trụ có chiều cao \(h = 2r\) và bán kính đáy \(R = 2r\).
\( \Rightarrow \) Thể tích khối trụ là \(V = \pi {\left( {2r} \right)^2}2r = 8\pi {r^3} = 120 \Leftrightarrow {r^3} = \dfrac{{120}}{{8\pi }} = \dfrac{{15}}{\pi }\).
Vậy thể tích mỗi khối cầu là \({V_c} = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi .\dfrac{{15}}{\pi } = 20\,\,\left( {c{m^3}} \right)\).
Cho hình trụ bán kính đường tròn đáy bằng 1. Hai điểm \(A\) và \(B\) lần lượt thuộc hai đường tròn đáy sao cho \(AB = \sqrt 6 \), khoảng cách giữa hai đường thẳng \(AB\) và trục của hình trụ bằng \(\dfrac{1}{2}\). Thể tích khối trụ được giới hạn bởi hình trụ đó bằng:
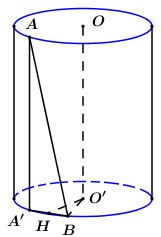
Gọi \(O,\,\,O'\) lần lượt là tâm đường tròn đáy chứa \(A,\,\,B\).
Gọi \(A'\) là hình chiếu của \(A\) lên đường tròn đáy chứa điểm \(B\).
Ta có \(AA'\parallel OO' \Rightarrow OO'\parallel \left( {AA'B} \right) \supset AB\) \( \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {AA'B} \right)} \right) = d\left( {O';\left( {AA'B} \right)} \right)\).
Gọi \(H\) là trung điểm của \(A'B\), ta có \(O'H \bot A'B\) (quan hệ vuông góc giữa đường kính và dây cung).
Khi đó ta có: \(\left\{ \begin{array}{l}O'H \bot A'B\\O'H \bot AA'\end{array} \right. \Rightarrow O'H \bot \left( {AA'B} \right)\) \( \Rightarrow d\left( {OO';AB} \right) = OH = \dfrac{1}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(O'HB\) có \(HB = \sqrt {O'{B^2} - O'{H^2}} = \sqrt {{1^2} - {{\left( {\dfrac{1}{2}} \right)}^2}} = \dfrac{{\sqrt 3 }}{2}\).
\( \Rightarrow A'B = 2HB = \sqrt 3 \).
Áp dụng định lí Pytago trong tam giác vuông có: \(AA' = \sqrt {A{B^2} - A'{B^2}} = \sqrt {6 - 3} = \sqrt 3 \).
Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi {.1^2}.\sqrt 3 = \pi \sqrt 3 \).
Trong không gian \(Oxyz\), tập hợp các điểm \(M\left( {a;b;c} \right)\) sao cho \({a^2} + {b^2} \le 2,\,\,\left| c \right| \le 8\) là một khối tròn xoay. Tính thể tích của khối tròn xoay đó?
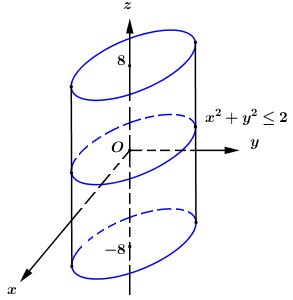
Tập hợp các điểm \(M\left( {a;b;c} \right)\) sao cho \({a^2} + {b^2} \le 2,\,\,\left| c \right| \le 8\) là khối trụ có bán kính đáy \(r = \sqrt 2 \), chiều cao \(h = 16\).
Do đó thể tích khối trụ là \(V = \pi {r^2}h = \pi .{\left( {\sqrt 2 } \right)^2}.16 = 32\pi \).
Một hình trụ có diện tích xung quanh là \(16\pi \), thiết diện qua trục là hình vuông. Một mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo thiết diện là \(ABB'A'\), biết một cạnh thiết diện là một dây của đường tròn đáy hình trụ và căng một cung \({120^0}\). Chu vi tứ giác \(ABB'A'\) bằng:
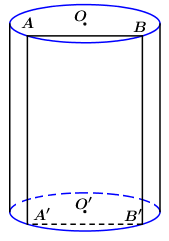
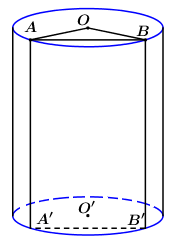
Gọi \(r,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ, ta có \({S_{xq}} = 2\pi rh \Leftrightarrow 16\pi = 2\pi rh \Leftrightarrow rh = 8\).
Lại có thiết diện qua trục là hình vuông nên \(h = 2r\), do đó \(r.2r = 8 \Leftrightarrow {r^2} = 4\) \( \Rightarrow r = 2,\,\,h = 4 = AA'\).
Theo bài ra ta có: \(\angle AOB = {120^0}\).
Áp dụng định lí Cosin trong tam giác \(OAB\) ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \angle AOB\\A{B^2} = {r^2} + {r^2} - 2.r.r.\cos {120^0}\\A{B^2} = 3{r^2}\\ \Rightarrow AB = r\sqrt 3 = 2.\sqrt 3 \end{array}\)
Vậy \({C_{ABB'A'}} = 2\left( {AB + AA'} \right) = 2\left( {2\sqrt 3 + 4} \right) = 8 + 4\sqrt 3 \).
Cho hình trụ có bán kính đáy bằng \(1\) và chiều cao bằng \(3\). Thiết diện của hình trụ cắt bởi mặt phẳng qua trục của nó có diện tích bằng:
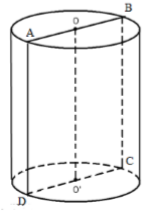
Giả sử thiết diện qua trục là hình chữ nhật \(ABCD\), ta có \(AD = h = 3,\,\,AB = 2r = 2\).
Vậy \({S_{ABCD}} = 3.2 = 6\).
Cho khối trụ có hai đáy là \(\left( O \right)\) và \(\left( {O'} \right)\). \(AB,\,\,CD\) lần lượt là hai đường kính của \(\left( O \right)\) và \(\left( {O'} \right)\), góc giữa \(AB\) và \(CD\) bằng \({30^0}\), \(AB = 6\) và thể tích khối tứ diện \(ABCD\) bằng 30. Thể tích khối trụ đã cho bằng:
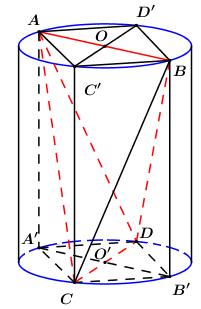
Gọi \(A',\,\,B'\) lần lượt là hình chiếu của \(A,\,\,B\) lên đường tròn \(\left( O \right)\).
\(C',\,\,D'\) lần lượt là hình chiếu của \(C,\,\,D\) lên đường tròn \(\left( {O'} \right)\).
\( \Rightarrow AC'BD'\) là hình bình hành, lại có \(AB = CD = C'D'\) nên \(AC'BD'\) là hình chữ nhật.
Khi đó \(AC'BD'.A'CB'D\) là hình hộp chữ nhật.
Ta có: \({V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\).
Ta có: \({V_{A.A'CD}} = \dfrac{1}{3}AA'.{S_{A'CD}} = \dfrac{1}{3}AA'.\dfrac{1}{2}{S_{A'CB'D}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
CMTT ta có: \({V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
\(\begin{array}{l} \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4.\dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\\ \Rightarrow {V_{ABCD}} = \dfrac{1}{3}{V_{AC'BD'.A'CB'D}} = 30\\ \Rightarrow {V_{AC'BD'.A'CB'D}} = 90\end{array}\)
Theo bài ra ta có: \(\angle \left( {AB;CD} \right) = {30^0} \Rightarrow \angle \left( {AB;C'D'} \right) = {30^0}\), giả sử \(\angle \left( {AB;C'D'} \right) = \angle AOC' = {30^0}\).
Lại có \(OA = OC' = \dfrac{1}{2}AB = 3\) \( \Rightarrow {S_{OAC'}} = \dfrac{1}{2}OA.OC'.\sin \angle AOC' = \dfrac{1}{2}.3.3.\sin {30^0} = \dfrac{9}{4}\).
\( \Rightarrow {S_{AC'BD'}} = 4{S_{OAC'}} = 9\).
Ta có: \({V_{AC'BD'.A'CB'D}} = AA'.{S_{AC'BD'}}\)\( \Rightarrow 90 = AA'.9 \Leftrightarrow AA' = 10\).
Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi .O{A^2}.AA' = \pi {.3^2}.10 = 90\pi \).
Cho hình trụ có \(O,\,\,O'\) là tâm hai đáy. Xét hình chữ nhật \(ABCD\) có \(A,\,\,B\) cùng thuộc \(\left( O \right)\) và \(C,\,\,D\) cùng thuộc \(\left( {O'} \right)\) sao cho \(AB = a\sqrt 3 \), \(BC = 2a\) đồng thời \(\left( {ABCD} \right)\) tạo với mặt phẳng đáy hình trụ góc \({60^0}\). Thể tích khối trụ bằng:
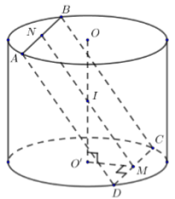
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(CD,\,\,AB\) và \(I\) là trung điểm của \(OO'\).
Ta có:
\(\left\{ \begin{array}{l}\left( {ABCD} \right) \cap \left( {O'CD} \right) = CD\\IM \subset \left( {ABCD} \right),\,\,IM \bot CD\\O'M \subset \left( {O'CD} \right),\,\,O'M \bot CD\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABCD} \right);\left( {O'BC} \right)} \right) = \angle \left( {IM;O'M} \right) = \angle IMO' = {60^0}\).
Ta có: \(MN = BC = 2a\) \( \Rightarrow IM = \dfrac{1}{2}MN = a\).
Xét tam giác vuông \(O'IM\) có: \(O'M = IM.\cos {60^0} = \dfrac{a}{2}\), \(O'I = IM.\sin {60^0} = \dfrac{{a\sqrt 3 }}{2}\).
\( \Rightarrow \) Chiều cao của khối trụ là \(h = OO' = 2O'I = a\sqrt 3 \).
Áp dụng định lí Pytago trong tam giác vuông \(O'CM\) có: \(O'C = \sqrt {O'{M^2} + C{M^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{3{a^2}}}{4}} = a\).
\( \Rightarrow \) Bán kính đáy của khối trụ là \(r = O'C = a\).
Vậy thể tích của khối trụ là: \(V = \pi {r^2}h = \pi .{a^2}.a\sqrt 3 = \pi {a^3}\sqrt 3 \).
Thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng 10. Diện tích xung quanh của hình trụ đó bằng:
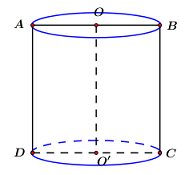
Ta có: \({S_{ABCD}} = AB.AD = 2rh = 10.\)
\( \Rightarrow {S_{xq}} = 2\pi rh = 10\pi .\)
Một cái nồi có dạng hình trụ có chiều cao 60cm và diện tích đáy là \(900\pi \,\,c{m^2}\). Hỏi cần miếng kim loại hình chữ nhật có kích thước bao nhiêu để làm thân nồi?
Ta có hình trụ có diện tích đáy là \(S = \pi {R^2} = 900\pi \Leftrightarrow R = 30\,\,cm\).
Diện tích xung quanh hình trụ là \(S = 2\pi Rh = 2\pi .30.60 = 60\pi .60\,\,\left( {c{m^2}} \right).\)
Vậy cần miếng kim loại hình chữ nhật chiều dài \(60\pi cm\) và chiều rộng \(60\, cm\)
Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \dfrac{2}{\pi }\,\,cm\) (như hình vẽ).
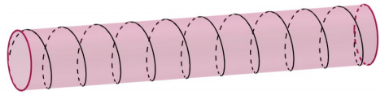
Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.
Gọi độ dài đường cao của ống trụ là \(10x\,\,\left( {cm} \right)\,\,\left( {x > 0} \right)\).
Chia ống trụ thành 10 phần bằng nhau, mỗi phần có độ dài đường sinh là \(x\,\,\left( {cm} \right)\).
Trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật có hai kích thước là \(x\) và \(2\pi .R = 2\pi .\dfrac{2}{\pi } = 4\,\,\left( {cm} \right)\).
Khi đó độ dài đường chéo của hình chữ nhật là \(\sqrt {{x^2} + {4^2}} = \sqrt {{x^2} + 16} \), và độ dài đường chéo chính bằng độ dài của 1 vòng.
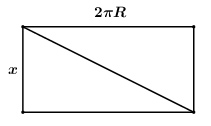
Do đó ta có phương trình: \(10\sqrt {{x^2} + 16} = 50 \Leftrightarrow \sqrt {{x^2} + 16} = 5\) \( \Rightarrow {x^2} + 16 = 25 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = 3\,\,\left( {cm} \right)\,\,\left( {tm} \right)\).
\( \Rightarrow \) Độ dài đường cao của ống trụ là \(h = 10x = 30\,\,\left( {cm} \right)\).
Vậy diện tích xung quanh của ống trụ là \({S_{xq}} = 2\pi Rh = 2\pi .\dfrac{2}{\pi }.30 = 120\,\,\left( {c{m^2}} \right)\).
Cho tứ diện đều ABCD có cạnh bằng 4. Hình trụ \(\left( T \right)\) có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. Diện tích xung quanh của \(\left( T \right)\) bằng:
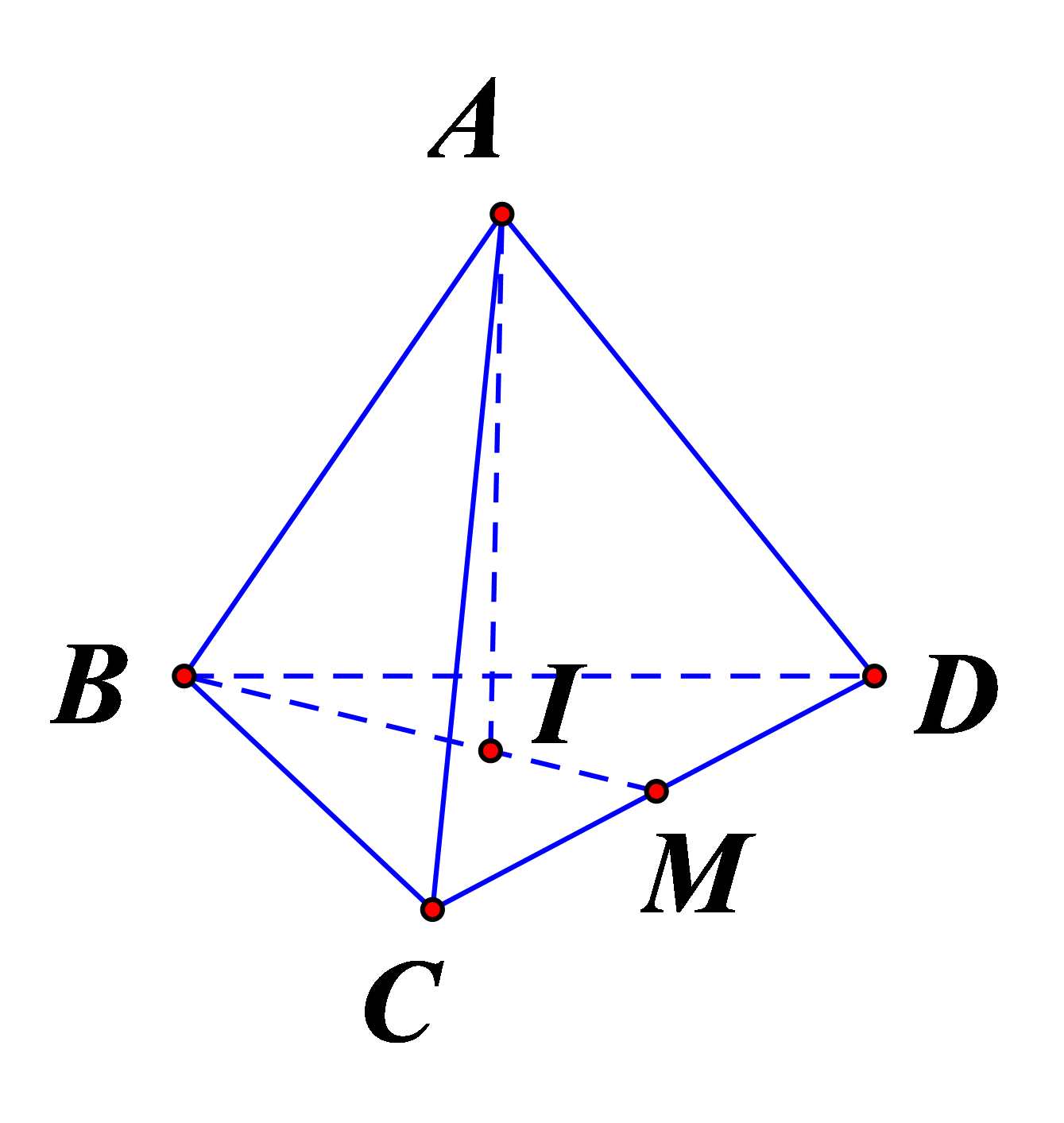
Tam giác BCD là tam giác đều cạnh 4\( \Rightarrow \left\{ \begin{array}{l}{S_{BCD}} = 4\sqrt 3 \\p = 12\end{array} \right.\)
Áp dụng công thức tính bán kính đường tròn nội tiếp ta có:\(R = \dfrac{{2S}}{p} = \dfrac{{2\sqrt 3 }}{3}\)
Gọi O là tâm của tam giác đều BCD
\( \Rightarrow AO \bot \left( {BCD} \right) \Rightarrow \Delta ABO\) vuông tại O có \(BO = \dfrac{{4\sqrt 3 }}{3};AB = 4 \Rightarrow AO = h = \dfrac{{4\sqrt 6 }}{3}\)
Khi đó diện tích xung quanh hình trụ có \(h = \dfrac{{4\sqrt 6 }}{3};R = \dfrac{{2\sqrt 3 }}{3}\) là \(S = 2\pi Rh = \dfrac{{16\sqrt 2 \pi }}{3}\)

