Diện tích hình trụ, thể tích khối trụ

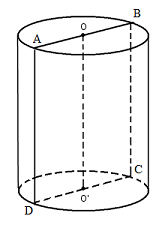
Gọi \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ.

Giả sử thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật \(ABCD\) như hình vẽ, ta có \(AB = 2R\) và \(AD = h\).

Chu vi thiết diện chứa trục bằng 12 \( \Rightarrow 2R + h = 6 \Rightarrow h = 6 - 2R\).

Khi đó thể tích khối trụ:

\(\begin{array}{l}V = \pi {R^2}h = \pi {R^2}\left( {6 - 2R} \right) = \pi .R.R\left( {6 - 2R} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \le \pi .{\left( {\dfrac{{R + R + 6 - 2R}}{3}} \right)^3} = 8\pi \end{array}\)

Dấu “=” xảy ra khi và chỉ khi \(R = 6 - 2R \Leftrightarrow R = 2.\)

Vậy thể tích khối trụ lớn nhất là \(8\pi \) khi \(R = 2\).

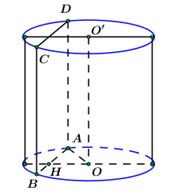
Mặt phẳng \(\left( \alpha  \right)\) song song với trục, cắt hình trụ theo thiết diện là một hình chữ nhật \(ABCD\) với \(AD = BC = h = 5.\)  

\( \Rightarrow 2\left( {AB + BC} \right) = 2\left( {AB + 5} \right) = 26 \Leftrightarrow AB = 8\,\,cm.\)

Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB \Rightarrow OH \bot \left( {ABCD} \right)\) hay \(OH \bot \left( \alpha  \right).\)  

\( \Rightarrow d\left( {OO';\,\,\left( \alpha  \right)} \right) = d\left( {O;\,\,\left( \alpha  \right)} \right) = OH.\)

\( \Rightarrow AH = \frac{{AB}}{2} = 4\,\,cm.\)

Áp dụng định lý Pitago cho \(\Delta AOH\) vuông tại \(H\) ta có:

\(\begin{array}{l}OH = \sqrt {O{A^2} - A{H^2}}  = \sqrt {{5^2} - {4^2}}  = 3cm.\\ \Rightarrow d\left( {OO';\,\,\left( \alpha  \right)} \right) = 3\,cm.\end{array}\)