Cho hình thoi \(ABCD\) có \(BD = 60cm,AC = 80cm.\) Vẽ các đường cao \(BE\) và \(BF.\) Tính diện tích tứ giác \(BEDF.\)
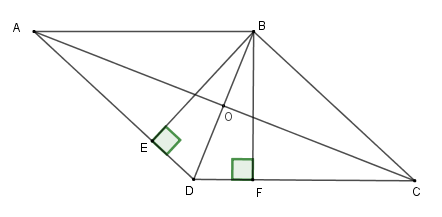
Gọi \(O\) là giao điểm của \(AC,BD.\)
Vì \(ABCD\) là hình thoi nên \(AC \bot BD;OA = OC = \dfrac{{AC}}{2} = 40cm;\) \(OB = OD = \dfrac{{BD}}{2} = 30\,cm\).
Xét tam giác vuông \(AOB,\) theo định lý Pytago ta có: \(A{B^2} = O{A^2} + O{B^2} = {40^2} + {30^2} = 2500 \Rightarrow AB = 50\,cm\).
Lại có: \({S_{ABCD}} = \dfrac{{AC.BD}}{2} = \dfrac{{60.80}}{2} = 2400\,c{m^2}\) mà \({S_{ABCD}} = BE.AD \Leftrightarrow BE.50 = 2400 \Leftrightarrow BE = 48\,cm\) (vì \(AD = AB = 50cm\)).
Xét tam giác vuông \(BED\) có: \(E{D^2} = B{D^2} - B{E^2} = {60^2} - {48^2} = 1296\) \( \Rightarrow ED = 36\).
Suy ra: \({S_{BED}} = \dfrac{1}{2}DE. BE = \dfrac{1}{2}48. 36 = 864\,c{m^2}\).
Lại có: \(\Delta BED = \Delta BFD\left( {ch - gn} \right)\) nên \({S_{BFD}} = {S_{BED}} = 864\,c{m^2}\).
Từ đó: \({S_{BEDF}} = {S_{BED}} + {S_{BFD}} = 864 + 864 = 1728\,c{m^2}.\)
