Tính thể tích của một hình lập phương, biết rằng đường chéo của hình lập phương bằng $\sqrt {12} cm$.
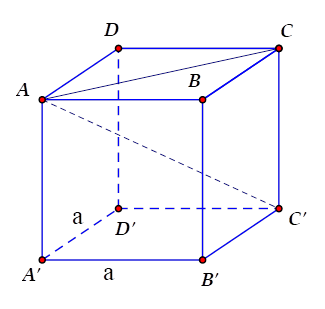
Gọi $a$ là cạnh của hình lập phương. Theo định lý Pitago ta có $AC^2=AB^2+BC^2=a^2+a^2$ suy ra $AC^2+CC'^2$\(={a^2} + {a^2} + {a^2} \)\(=A{C'^2} = {\left( {\sqrt {12} } \right)^2} = 12\)
Từ đó $a = 2\left( {cm} \right).$ Thể tích của hình lập phương bằng \(2^3=8\left( {c{m^3}} \right)\) .
Một hình hộp chữ nhật có đường chéo lớn bằng $17cm$ , các kích thước của đáy bằng $9cm$ và $12cm$ . Tính thể tích của hình hộp chữ nhật đó.
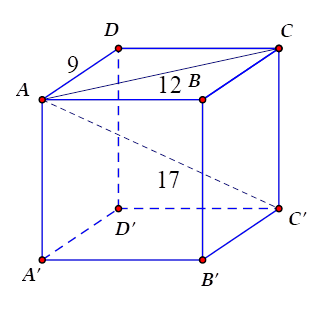
Vì \(ABCD\) là hình chữ nhật nên \(AD = BC = 9\,cm;\,AB = DC = 12\,cm\) .
Áp dụng định lý Pytago cho tam giác vuông \(ADC\) ta được:
\(AC = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{12}^2} + {9^2}} = 15\,cm\)
Ta có \(CC' \bot \left( {ABCD} \right)\) nên \(CC' \bot CD\) .
Áp dụng định lý Pytago cho tam giác vuông \(AC'C\) ta được:
\(CC' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {{{17}^2} - {{15}^2}} = 8\,cm\)
Thể tích của hình hộp chữ nhật bằng
\(9.12.8 = 864\left( {c{m^3}} \right)\)
Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài $80c$ m, chiều rộng $50$ cm. Mực nước trong bể cao $35$ cm. Người ta cho vào bể một hòn đá thì thể tích tăng $20000\,\,c{m^3}$ . Hỏi mực nước trong bể lúc này cao bao nhiêu?
Thể tích phần bể chứa nước ban đầu là:
$V = 80.50.35 = 140000\;c{m^3}$
Sau khi cho vào một hòn đá thể tích tăng $20000$ $cm^3$. Vậy thể tích phần bể chứa nước lúc sau là:
${V_1} = V + 20000 = 140000 + 20000 = 160000\;c{m^3}$
Vì chiều dài và chiều rộng bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi.
Gọi chiều cao mực nước lúc sau là $h$ cm. Ta có:
$V = 80.50.h = 160000 $$\Rightarrow h = \dfrac{V}{{80.50}} = \dfrac{{160000}}{{80.50}} = 40\;cm$
Một người thuê sơn mặt trong và mặt ngoài của $1$ cái thùng sắt không nắp dạng hình lập phương có cạnh $0,8$ m. Biết giá tiền mỗi mét vuông là $15000$ đồng. Hỏi người ấy phải trả bao nhiêu tiền?
Thùng sắt (không nắp) có dạng hình lập phương \( \Rightarrow \)Thùng sắt có 5 mặt bằng nhau.
Diện tích một mặt thùng sắt là:
\(S = 0,{8^2} = 0,64\;{m^2}\)
Ta có diện tích mặt trong thùng sắt bằng diện tích mặt ngoài thùng sắt. Vậy diện tích mặt trong và mặt ngoài thùng sắt là:
\({S_{mt}} = {S_{mn}} = 5S = 5.0,64 = 3,2\;{m^2}\)
Số tiền người thuê sơn thùng sắt cần trả là:
\(({S_{mt}} + {S_{mn}}).15000 = (3,2 + 3,2).15000 = 6,4.15000 = 96000\) đồng.

