Phương trình lượng giác cơ bản

Bước 1:

$\cos 11x\cos 3x = \cos 17x\cos 9x$

\( \Leftrightarrow \dfrac{1}{2}.\left[ {\cos \left( {11x + 3x} \right) + \cos \left( {11x - 3x} \right)} \right]\)\( = \dfrac{1}{2}\left[ {\cos \left( {17x + 9x} \right) + \cos \left( {17x - 9x} \right)} \right]\)

$\Leftrightarrow \dfrac{1}{2}\left( {\cos 14x + \cos 8x} \right) = \dfrac{1}{2}\left( {\cos 26x + \cos 8x} \right)\\ \Leftrightarrow \cos 14x + \cos 8x = \cos 26x + \cos 8x\\ \Leftrightarrow \cos 14x = \cos 26x$

Bước 2:

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}26x = 14x + k2\pi \\26x =  - 14x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}12x = k2\pi \\40x = k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{6}\\x = \dfrac{{k\pi }}{{20}}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)

Vậy nghiệm của phương trình là \(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\).

Ta có:

\(\begin{array}{l}\tan \left( {2x - {{15}^0}} \right) = 1 = \tan {45^0}\\ \Leftrightarrow 2x - {15^0} = {45^0} + k{180^0}\\ \Leftrightarrow 2x = {60^0} + k{180^0}\\ \Leftrightarrow x = {30^0} + k{90^0}\end{array}\)

Theo bài ra ta có:

\(\begin{array}{l} - {90^0} < x < {90^0}\\ \Leftrightarrow  - {90^0} < {30^0} + k{90^0} < {90^0}\\ \Leftrightarrow  - {120^0} < k{90^0} < {60^0}\\ \Leftrightarrow  - \dfrac{4}{3} < k < \dfrac{2}{3}\end{array}\)

Mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0; - 1} \right\}\).

Với \(k = 0\) ta có nghiệm \(x = {30^0}\).

Với \(k =  - 1\) ta có nghiệm \(x = {30^0} - {90^0} =  - {60^0}\).

Vậy phương trình đã cho có 2 nghiệm thỏa mãn là \(x =  - {60^0},\,\,x = {30^0}\).

Ta có: \(\cot 20x = 1 \Leftrightarrow 20x = \dfrac{\pi }{4} + k\pi \) \( \Leftrightarrow x = \dfrac{\pi }{{80}} + \dfrac{{k\pi }}{{20}}\,\,\left( {k \in \mathbb{Z}} \right)\).

Theo bài ra ta có:

\(\begin{array}{l}x \in \left[ { - 50\pi ;0} \right]\\ \Leftrightarrow  - 50\pi  \le \dfrac{\pi }{{80}} + \dfrac{{k\pi }}{{20}} \le 0\\ \Leftrightarrow  - 50 \le \dfrac{1}{{80}} + \dfrac{k}{{20}} \le 0\\ \Leftrightarrow  - \dfrac{{4001}}{4} \le k \le  - \dfrac{1}{4}\\ \Leftrightarrow  -1000,25 \le k \le  - 0,25\end{array}\)

Mà \(k \in \mathbb{Z}\)\( \Rightarrow -1000 \le k \le -1\)

\( \Rightarrow k \in \left\{ { - 1000; - 999;....; - 2; - 1} \right\}\)

Tập trên có $-1-(-1000)+1=1000$ phần tử suy ra có $1000$ giá trị nguyên của $k$ thỏa mãn.

Vậy phương trình đã cho có $1000$ nghiệm thỏa mãn yêu cầu bài toán.

ĐK: \(\left\{ \begin{array}{l}\sin x \ne 0\\\sin 2x \ne 0\end{array} \right. \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow 2x \ne k\pi  \Leftrightarrow x \ne \frac{{k\pi }}{2}\,\,\left( {k \in Z} \right)\).

\(\cot x = \cot 2x \Leftrightarrow 2x = x + k\pi  \Leftrightarrow x = k\pi \,\,\left( {k \in Z} \right)\,\,\,\left( {ktm} \right)\).

Vậy phương trình đã cho vô nghiệm.

Hàm số \(y = \dfrac{{2\sin x - 1}}{{\tan 2x + \sqrt 3 }}\) xác định khi

\(\left\{ \begin{array}{l}{\rm{cos2}}x \ne 0\\\tan 2x \ne  - \sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x \ne \dfrac{\pi }{2} + k\pi \\2x \ne \dfrac{{ - \pi }}{3} + k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{4} + k\dfrac{\pi }{2}\,\\x \ne \dfrac{-\pi }{6} + k\dfrac{\pi }{2}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

Ta có: \(\cos 2x = \dfrac{1}{2} \Leftrightarrow \cos 2x = cos\dfrac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{3} + k2\pi \\2x =  - \dfrac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow x =  \pm \dfrac{\pi }{6} + k\pi \,\,\,\left( {k \in \mathbb{Z}} \right).\)

Trên nửa khoảng \(\left( {{0^0};{{360}^0}} \right]\)tức \(\left( {0;2\pi } \right]\). Ta sẽ có các nghiệm thỏa mãn như sau:

\( + )\,\,\,0 < x = \dfrac{\pi }{6} + k\pi  \le 2\pi  \Leftrightarrow  - \dfrac{1}{6} < k \le \dfrac{{11}}{6}\) mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1} \right\}\). Có 2 nghiệm.

\( + )\,\,\,0 < x =  - \dfrac{\pi }{6} + k\pi  \le 2\pi  \Leftrightarrow \dfrac{1}{6} < k \le \dfrac{{13}}{6}\) mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2} \right\}\). Có 2 nghiệm.

Vậy có 4 nghiệm thỏa mãn yêu cầu bài toán.

Bước 1:

Với \(x \in \left( {0;\dfrac{\pi }{6}} \right] \Rightarrow 3x \in \left( {0;\dfrac{\pi }{2}} \right]\).

Hàm số \(y = \cos x\) nghịch biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\) nên ta có:

\(0 < 3x \le \dfrac{\pi}{2} \Leftrightarrow \cos \dfrac{\pi}{2} \le \cos 3x \le \cos 0 \Leftrightarrow 0 \le \cos 3x < 1\)

Bước 2:

Do đó phương trình \(\cos 3x = 2{m^2} - 3m + 1\) có nghiệm khi và chỉ khi:

\(0 \le 2{m^2} - 3m + 1 < 1\)

\(\Leftrightarrow \left\{ \matrix{
2{m^2} - 3m + 1 \ge 0 \hfill \cr
2{m^2} - 3m + 1 < 1 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{
\left[ \matrix{
m \ge 1 \hfill \cr
m \le \dfrac{1}{2} \hfill \cr} \right. \hfill \cr
0 < m < \dfrac{3}{2} \hfill \cr} \right. \)

Kết hợp nghiệm:

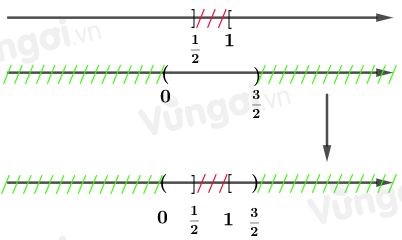
\(\Leftrightarrow m \in \left( {0;\dfrac{1}{2}} \right] \cup \left[ {1;\dfrac{3}{2}} \right)\)

Thay \(x = \dfrac{{11\pi }}{{60}}\) vào phương trình ta có:

\(\begin{array}{l}\sin \left( {2.\dfrac{{11\pi }}{{60}} - \dfrac{\pi }{5}} \right) = 3{m^2} + \dfrac{m}{2} \Leftrightarrow \sin \dfrac{\pi }{6} = 3{m^2} + \dfrac{m}{2}\\ \Leftrightarrow \dfrac{1}{2} = 3{m^2} + \dfrac{m}{2} \Leftrightarrow 6{m^2} + m = 1 \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{3}\\m =  - \dfrac{1}{2}\end{array} \right.\end{array}\)

ĐKXĐ: \(\sin x - \dfrac{1}{2} \ne 0 \Rightarrow \sin x \ne \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x \ne \dfrac{\pi }{6} + k2\pi \\x \ne \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

\(\dfrac{{\cos x - \dfrac{{\sqrt 3 }}{2}}}{{\sin x - \dfrac{1}{2}}} = 0 \Leftrightarrow \cos x - \dfrac{{\sqrt 3 }}{2} = 0 \Leftrightarrow \cos x = \dfrac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x =  - \dfrac{\pi }{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

Đối chiếu ĐKXĐ ta thấy chỉ có nghiệm \(x =  - \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) thỏa mãn.

Vậy nghiệm của phương trình là \(x =-  \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

Phương trình \(\sin \left( {2x + \dfrac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm khi và chỉ khi:

\(\left[ \begin{array}{l}{m^2} - 3m + 3 > 1\\{m^2} - 3m + 3 <  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} - 3m + 2 > 0\\{m^2} - 3m + 4 < 0\,\,\left( {vo\,\,nghiem} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\).

\(\begin{array}{l}\sin \left( {\dfrac{\pi }{3} - 3x} \right) = \sin \left( {x + \dfrac{\pi }{4}} \right) \Leftrightarrow \left[ \begin{array}{l}\dfrac{\pi }{3} - 3x = x + \dfrac{\pi }{4} + k2\pi \\\dfrac{\pi }{3} - 3x = \pi  - x - \dfrac{\pi }{4} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} - 4x =  - \dfrac{\pi }{{12}} + k2\pi \\ - 2x = \dfrac{{5\pi }}{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{{48}} + \dfrac{{k\pi }}{2}\\x =  - \dfrac{{5\pi }}{{24}} + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)